سری فوریه کاربرد
کاربرد سری فرویه
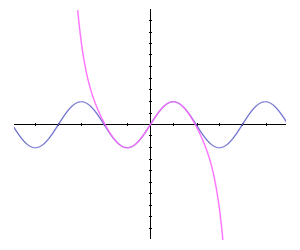
کاربرد سری فوریه سری فوریه توسعه نظریه سریهای مثلثاتی در 1822 ،با چاپ کتابی توسط فوریه آغاز شد.تحقیقات چندین ساله وی به گسترش نظریه وسیعی در مورد سریها منجر شدکه امروزه به نام خود وی معروف ،و از اهمیت بسیاری در ریاضیات ،علوم و فن برخوردار است.ایده اساسی این نظریه،معرفی توابع تناوبی یا دوره ای توسط توابع تناوبی(مثلثاتی) خاص است. سری فوریه برای بررسی حرکات تناوبی در آکوستیک یا صوت شناسی،الکترودینامیک ،اپتیک یا نور شناسی، ترمودینامیک و غیره مورد استفاده قرار گرفته است. در مهندسی الکتریک مسائلی چون رفتار بسامدی ،عناصر سوئیچینگ ،یا انتقال ضربه ها را میتوان به کمک سری فوریه حل کرد. پیش بینی جزرومد در دریانوردی دارای اهمیت فراوانی است.از آنجا که اینها پدیده هایی تناوبی هستند از سری فوریه استفاده میشود و در تمام بندرهای مهم،وسائل مکانیکی چون پیش بینی کننده های جزر و مد ساخته میشود.امروزه کمتر شاخهای از فیزیک،ریاضیات، یا صنعت و فن وجود دارد که در آن از سریهای فوریه استفاده نشود. تعریف سری توابع که جمله عمومی آن با ضرایب ثابت و است سری مثلثاتی نامیده میشود. اگر این سری در بازهای از طول همگرا باشد،آنگاه از آنجا که توابع مثلثاتی تناوبی اند، به ازای جمیع مقادیر x همگراست و تابع تناوبی ی را نشان میدهد. این تابع لزوما پیوسته نیست، و در واقع اغلب بین آنچه که توسط فرمول های مختلف داده شده است گسستگی هایی دارد. از طرف دیگر،اگر این سری به طور یکنواخت همگرا باشد،آنگاه مجموع آن، ،پیوسته است. در این حالت میتوان ارتباطی بین ضرایب و و تابع مجموع به دست آورد.ضرب سری در عاملهای کراندار یا که در آنها p عددی صحیح و نامنفی است اختلالی در همگرایی یکنواخت آن به وجود نمی آورد،بنابراین میتوان و را با استفاده از انتگرالگیری جمله به جمله سری یا محاسبه کرد این انتگرالگیری ها شامل انتگرال های روی بازه توابع و و و اند. به نقل از : http://iauh-ms1.blogfa.com
ریاضی مهندسی و سری فوریه

ریاضی مهندسی(به زبان لاتین) ریاضی مهندسی(به زبان لاتین) ریاضی مهندسی(به زبان لاتین) ریاضیات عالی مهندسی-ریاضی مهندسی پیشرفته(به زبان لاتین) ریاضی مهندسی پیشرفته(آقای دکتر کاظم قنبری) ریاضی مهندسی(آقای دکتر معتقدی) ریاضی مهندسی(آقای دکتر پوررضا) ریاضی مهندسی(آقای دکتر شیدفر) ریاضی مهندسی ریاضی مهندسی و لاپلاس(آقای دکتر سیاهی) جزوه سری فوریه مثال های حل شده از سری فوریه(به زبان لاتین) سری فوریه و سیستم های دیفرانسیل(به زبان لاتین) سری فوریه(به زبان لاتین) سری فوریه و تبدیل لاپلاس
سری فوریه
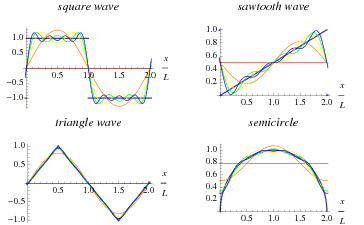
سری فوریه عبارت است از بسط تابع تناوبی در قالب جملاتی از جمع نامتناهی کسینوس ها و سینوس ها. در واقع سری فوریه بر کاربرد روابط تعامد (orthogonality relationships) توابع سینوسی و کسینوسی تاکید دارد. محاسبه و مطالعه ی سری های فوریه موسوم به آنالیز هارمونیک (harmonic analysis) می باشد که به عنوان یک روش بسیار سودمند برای تفکیک یک تابع تناوبی دلخواه به مجموعه ای از جملات ساده بوده که به راحتی می توان آنها را فهمید، منحصرا حل کرد و دوباره با ترکیب آنها راه حل مساله ی اولیه را بدست آورد، یا اینکه یک تقریب مطلوب و مناسبی را برای آن تخمین زد. نمونه هایی از تقریب های متوالی برای توابع معمول در ریاضیات با استفاده از سری های فوریه در شکل بالا گرداوری شده است. به ویژه از آن جایی که با توجه به اصل انطباق (برهم نهی) مجموع پاسخ های یک معادله ی دیفرانسیلی معمولی همگن خطی خود راه حل معادله ی اولیه محسوب می شوند، چنانچه بک چنین معادله ای را بتوان برای یک خم سینوسی یکتا حل کرد، آنگاه راه حل یک تابع دلخواه را می توان فورا با استفاده از توصیف تابع اولیه در قالب یک سری فوریه بدست آورد که متعاقبا این رویه منجر به فهم راه حل هر یک از مولفه های منتسب به خم سینوسی می گردد. این تکنیک حتی در برخی موارد خاص که سری فوریه محصور به یک شکل محدود و بسته است، به راه حل های تحلیلی نیز می انجامد. هر مجموعه ای از توابعی که یک دستگاه متعامد (راست گوشه) کامل (complete orthogonal system) را تشکیل می دهند، یک سری فوریه ی تعمیم یافته (generalized Fourier series) متناظر دارند که شبیه به سری فوریه است. مثلاْ استفاده از تعامد ریشه های تابع بسل نوع اول (Bessel function of the first kind) به اصطلاح یک سری بسل ـ فوریه (Bessel function of the first kind) را بدست می دهد. محاسبه ی سری فوریه (معمول) بر پایه ی اتحاد های انتگرالی زیر است: که و نماد دلتای کرونکر است: با استفاده از متد سری فوریه تعمیم یافته (generalized Fourier series) سری فوریه ی معمول شامل جملات سینوسی و کسینوسی با قرار دادن و حاصل می شود. چون این توابع یک دستگاه متعامد کامل در بازه ی را ایجاد می کنند، سری فوریه تابع به صورت زیر داده می شود: که و ... n=۱،۲،۳ توجه کنید که عامل a0 در فرم خاصی نوشته شده است که در قیاس با شکل عمومی سری فوریه تعمیم یافته می تواند تقارن نسبت به تعاریف an و bn را حفظ کند. اگر یک تابع شرایط دیریشله (Dirichlet conditions) را تصدیق کند، سری فوریه تابع مزبور همگرا به تابع می باشد که ...
سری فوریه
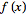
سری فوریه عبارت است از بسط تابع تناوبی در قالب جملاتی از جمع نامتناهی کسینوس ها و سینوس ها. در واقع سری فوریه بر کاربرد روابط تعامد (orthogonality relationships) توابع سینوسی و کسینوسی تاکید دارد. محاسبه و مطالعه ی سری های فوریه موسوم به آنالیز هارمونیک (harmonic analysis) می باشد که به عنوان یک روش بسیار سودمند برای تفکیک یک تابع تناوبی دلخواه به مجموعه ای از جملات ساده بوده که به راحتی می توان آنها را فهمید، منحصرا حل کرد و دوباره با ترکیب آنها راه حل مساله ی اولیه را بدست آورد... یا اینکه یک تقریب مطلوب و مناسبی را برای آن تخمین زد. نمونه هایی از تقریب های متوالی برای توابع معمول در ریاضیات با استفاده از سری های فوریه در شکل بالا گرداوری شده است.به ویژه از آن جایی که با توجه به اصل انطباق (برهم نهی) مجموع پاسخ های یک معادله ی دیفرانسیلی معمولی همگن خطی خود راه حل معادله ی اولیه محسوب می شوند، چنانچه بک چنین معادله ای را بتوان برای یک خم سینوسی یکتا حل کرد، آنگاه راه حل یک تابع دلخواه را می توان فورا با استفاده از توصیف تابع اولیه در قالب یک سری فوریه بدست آورد که متعاقبا این رویه منجر به فهم راه حل هر یک از مولفه های منتسب به خم سینوسی می گردد. این تکنیک حتی در برخی موارد خاص که سری فوریه محصور به یک شکل محدود و بسته است، به راه حل های تحلیلی نیز می انجامد.هر مجموعه ای از توابعی که یک دستگاه متعامد (راست گوشه) کامل (complete orthogonal system) را تشکیل می دهند، یک سری فوریه ی تعمیم یافته (generalized Fourier series) متناظر دارند که شبیه به سری فوریه است. مثلاْ استفاده از تعامد ریشه های تابع بسل نوع اول (Bessel function of the first kind) به اصطلاح یک سری بسل ـ فوریه (Bessel function of the first kind) را بدست می دهد.محاسبه ی سری فوریه (معمول) بر پایه ی اتحاد های انتگرالی زیر است: که و نماد دلتای کرونکر است:با استفاده از متد سری فوریه تعمیم یافته (generalized Fourier series) سری فوریه ی معمول شامل جملات سینوسی و کسینوسی با قرار دادن و حاصل می شود. چون این توابع یک دستگاه متعامد کامل در بازه ی را ایجاد می کنند، سری فوریه تابع به صورت زیر داده می شود: که و ... n=۱،۲،۳ توجه کنید که عامل a0 در فرم خاصی نوشته شده است که در قیاس با شکل عمومی سری فوریه تعمیم یافته می تواند تقارن نسبت به تعاریف an و bn را حفظ کند.اگر یک تابع شرایط دیریشله (Dirichlet conditions) را تصدیق کند، سری فوریه تابع مزبور همگرا به تابع می باشد که برابر با تابع اولیه در نقاط پیوستگی و یا میانگین دو حد در نقاط ناپیوستگی است، یعنیبه عنوان یک نتیجه، در نزدیکی ناپیوستگی ها، یک رشته ی حلقوی موسوم به پدیده ی گیبس (Gibbs phenomenon) می تواند اتفاق ...
سری فوریه (تکمیلی)
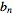
برای تابع متناوب در یک بازه مثل به جای ، یک تغییر ساده ی متغیرها می تواند برای تبدیل بازه ی انتگرالگیری از به مورد استفاده قرار بگیرد. فرض کنیم: با حل معادله اول نسبت به داریم ، لذا با وارد کردن این به خواهیم داشت: بنابراین: به طور یکسان، برای تابعی که در بازه ی تعریف می شود، معادلات بالا به سادگی به اشکال زیر تبدیل می شوند: در حقیقت برای تابع متناوب با دوره ی ، هر بازه ی با توجه به یکی از دو اصل راحتی یا اولویت شخصی می تواند بکار گرفته شود (Arfken 1985, p. 769). ضرایب (coefficients) برای بسط های سری های فوریه ی تعدادی از توابع مرسوم در Beyer, 1987, pp. 411-412 و Byerly, 1959, p. 51 آمده است. یکی از مرسوم ترین توابعی که با استفاده از تکنیک اخیر مورد تجزیه تحلیل قرار می گیرد، موج چهار گوش یا مربعی (square wave) است. سری های فوریه برای تعدادی از توابع مرسوم در جدول زیر گرداوری شده اند. تابع سری فوریه سری های فوریه---موج دندانه اره ای سری های فوریه---موج مربعی سری های فوریه---موج مثلثی اگر یک تابع زوج باشد، یعنی ، آنگاه زوج است. (این بدان خاطر است که چون فرد است و یک تابع زوج (even function) ضرب در یک تابع زوج برابر با یک تابع فرد (odd function) است.) بنابراین برای تمامی nها . به طور یکسان، اگر یک تابع فرد است، پس ، آنگاه فرد است. (این بدان خاطر است که چون زوج است و یک تابع زوج (even function) ضرب در یک تابع فرد برابر با یک تابع فرد (odd function) است.) بنابراین برای تمامی nها نظریه ی سری های فوریه همچنین می تواند به ضرایب مختلط (complex coefficients) بسط داده شود. یک تابع حقیقی-مقدار را در نظر می گیریم. می نویسیم: حال بررسی می کنیم که لذا ضرایب (coefficients) را می توان برحسب آنهایی که در سری های فوریه گفته شده اند، توضیح داد: برای یک تابع متناوب در ، اینها به شکل های زیر تبدیل خواهند شد: این معادلات مبنای مهمی برای شکل گیری تبدیل فوریه (Fourier transform) محسوب می شوند که با تبدیل از یک متغیر مجزا به یک متغیر پیوسته در طول بدست می آید. لینک مربوطه: سری فوریه منابع: Arfken, G. "Fourier Series." Ch. 14 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 760-793, 1985. Askey, R. and Haimo, D. T. "Similarities between Fourier and Power Series." Amer. Math. Monthly 103, 297-304, 1996. Beyer, W. H. (Ed.). CRC Standard Mathematical Tables, 28th ed. Boca Raton, ...
سری فوریه
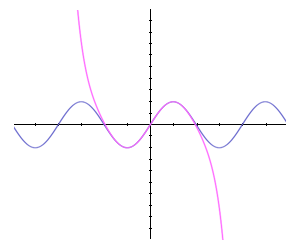
سری مثلثاتی یا فوریه توسعه نظریه سریهای مثلثاتی در 1822 ،با چاپ کتابی توسط فوریه آغاز شد.تحقیقات چندین ساله وی به گسترش نظریه وسیعی در مورد سریها منجر شدکه امروزه به نام خود وی معروف ،و از اهمیت بسیاری در ریاضیات ،علوم و فن برخوردار است.ایده اساسی این نظریه،معرفی توابع تناوبی یا دوره ای توسط توابع تناوبی(مثلثاتی) خاص است. سری فوریه برای بررسی حرکات تناوبی در آگوستیک یا صوت شناسی،الکترو دینامیک ،ایتیک یا نور شناسی، ترمودینامیک و غیره مورد استفاده قرار گرفته است. در مهندسی الکتریک مسائلی چون رفتار بسامدی ،عناصر سوئیچینگ ،یا انتقال ضربه ها را میتوان به کمک سری فوریه حل کرد. پیش بینی جزرومد در دریانوردی دارای اهمیت فراوانی است.از آنجا که اینها پدیده هایی تناوبی هستند از سری فوریه استفاده میشود و در تمام بندرهای مهم،وسائل مکانیکی چون پیش بینی کننده های جزر و مد ساخته میشود.امروزه کمتر شاخهای از فیزیک،ریاضیات، یا صنعت و فن وجود دارد که در آن از سریهای فوریه استفاده نشود. تعریف سری توابع که جمله عمومی آن با ضرایب ثابت و است سری مثلثاتی نامیده میشود. اگر این سری در بازهای از طول همگرا باشد،آنگاه از آنجا که توابع مثلثاتی تناوبی اند، به ازای جمیع مقادیر x همگراست و تابع تناوبی ی را نشان میدهد. این تابع لزوما پیوسته نیست، و در واقع اغلب بین آنچه که توسط فرمول های مختلف داده شده است گسستگی هایی دارد. از طرف دیگر،اگر این سری به طور یکنواخت همگرا باشد،آنگاه مجموع آن، ،پیوسته است. در این حالت میتوان ارتباطی بین ضرایب و و تابع مجموع به دست آورد.ضرب سری در عاملهای کراندار یا که در آنها p عدد صحیح و نامنفی است اختلالی در همگرایی یکنواخت آن به وجود نمی آورد،بنابراین میتوان و را با استفاده از انتگرالگیری جمله به جمله سری یا محاسبه کرد.این انتگرالگیری ها شامل انتگرال های روی بازه توابع و و و اند. سری فوریه ، روشی در ریاضیات میباشد که به وسیله آن ، هر تابع متناوبی به صورت جمعی از توابع سینوس و کسینوس میتواند نوشته شود. نام این قضیه به اسم ریاضیدان فرانسوی ، ژوزف فوریه ،ثبت شده است. در نظریه سریهای فوریه نشان داده شده است که اگر (f(x در شرایطی مثل (شرط دیریشله) صدق کند، میتوان آن را به صورت سری هماهنگی به شکل: بسط داد و اینکه در نقاط ناپیوستگی سری سمت راست رابطه فوق برابر مقدار متوسط است. ضرایب an و bn را میتوان با استفاده از روابط متعامد:که در آنها mnδ نماد کرونکر است که به ازای m=n برابر واحد و در غیر اینصورت صفر است. همچنین اگر یک تابع متناوب با تناوب T باشد یا به عبارتی: (f(t + T) = f(t آنگاه ، ...
سری فوریه
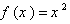
سری فوریه تابع را در بازه بیابید. حل:چون تابعی است زوج ، پس .ودر نتیجه ، سری فوریه تابع f برابر است با بنا به همگرایی یکنواخت سری فوق ، مقدار این سری در هر نقطه x برابر است با یعنیاگر در رابطه فوق ،قرار دهیم ، خواهیم داشت:از این رو و در اینجا حل مساله کامل است.لازم به توضیح می باشد که سری بدست آمده فوق ، به تابع زتا 2 معروف می باشدکه کاربرد زیادی نیز در ریاضیات دارد.
سری فوریه
سری فوریه در نظریه ی سری های فوریه نشان داده شده است که اگر در شرایطی مثل (شرط دیریشله) صدق کند،میتوان آن را به صورت سری هماهنگی به شکل بسط داد و اینکه در نقاط ناپیوستگی سری سمت راست رابطه ی فوق برابر مقدار متوسط است. ضرایب an و bn را می توان با استفاده از روابط متعامد ۰ ۰ ۰ که در آن ها نماد کرونکر است که به ازای m=n برابر واحد و در غیر اینصورت صفر است. همچنین که حساب کرد. میتوان نشان داد که این سری به طور یکنواخت در بازه ی (L/۲ , -L/۲) همگراست، به طوریکه انتگرال گیری جمله به جمله در استنتاج این معادلات کار بجایی است. این معادلات را با تبدیلات زیر ادامه می دهیم: در نتیجه: بنابراین حال با تغییر بازه ی انتگرال گیر فوق به داریم: این سری را می توان به صورت زیر هم نوشت: به عنوان آزمون بنابراین ضریب An را میتوان به صورت زیر توسعه داد: در نهایت در بازه سری فوریه به صورت و تعریف می شود.
سری فوریه
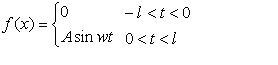
سری فوریه فرض کنید تابع f به صورت زیر تعریف شده یاشد. تابع f یک تابع تناوبی با دوره 2L می باشد و ثابتهای بسط فوریه این تابع از روایط زیر بدست می آیند برای محاسبه این ثوابت از دستور int استفاده می کنیم R = int(S)R = int(S,v)R = int(S,a,b)R = int(S,v,a,b) استفاده از این دستور ببسیار ساده است.S عبارتی است که می خواهیم از آن انتگرال بگیریم، v متغیر مستقل است و a,b حدود انتگرال گیری هستند اولین قدم برای استفاده از این دستور تعریف متغیرهاست syms w A t n و بعد از آن محاسبه ثوابت a0= w/pi*int('A*sin(w*t)','t',0,pi/w) an=w/pi*int('A*sin(w*t)*cos(n*w*t)','t',0,pi/w) bn=w/pi*int('A*sin(w*t)*sin(n*w*t)','t',0,pi/w) قدم بعدی یافتن مقدار ثوابت در n های مختلف است.برای این کار از دستور subs استفاده می کنیم subs(bn,n,3) دستور بالا مقدار bn را به ازای n=3 محاسبه می کند مقدار an را در n=1 مبهم است چون صورت و مخرج an صفر می شود .با استفاده از دستور limit حد این عبارت را در n=1 می توان بدست آورد. limit(an,n,1,'right') limit(an,n,1,'left') حتما می دانید که سری فوریه هر تابع، تقریبی از آن تابع است.هرچه چملات سری بیشتر باشد مقدار سری به مقدار واقعی تابع نزدیک تر است. یکی از راه های بدست آوردن سری فوریه یک تابع استفاده از دستور fit است.این دستور توانایی محاسبه سری فوریه با حداکثر 8 جمله را دارد. x=[-pi:.1:pi]'; y=sin(x); f=fit(x,y,'fourier1') به جای fourier1 می توان fourier2...fourier8 را قرار داد. توابع زیر هم نیاز معرفی ندارند/ تابع گاما Y = gamma(A) تابع خطا Y = erf(X) تبدیل فوریه، نامیده شده به اسم ریاضیدانِ فرانسوی ژوزف فوریه، یک انتقال انتگرالی است که هر تابع f(t) را به یک تابع دیگر F(ω) منعکس میکند. به F(ω) در این صورت تبدیلشده فوریه تابع f(t) میگویند. حالت خاص انتقال فوریه، سری فوریه نام دارد و آن زمانی کاربرد دارد که تابع f(t) متناوب باشد، یعنی: f(t + T) = f(t) . حال اگر تابع متناوب نباشد و یا به عبارتی، تناوب آن برابر بینهایت باشد ()، آنگاه از سری فوریه به راحتی، عبارت زیر به دست میآید: تبدیل فوریه و همراه آن آنالیز فوریه، در مباحث مختلف فیزیک، از جمله الکترونیک و الکترومغناطیس (به خصوص در پیغامرسانی و مخابرات)، آکوستیک، فیزیک امواج و غیره کاربرد فراوان دارد. برگرفته از سایت ویکی پدیا و آموزش مطلب
کاربرد سری فوریه در تحلیل مدارهای الکترونیکی

آنالیز فوریه در بسیاری از زمینه های علوم کاربرد وسیعی دارد از جمله ریاضیات و فیزیک و شیمی تا لرزه شناسی و پزشکی و ... در مهندسی برق یکی از کاربرد های سری فوریه یافتن پاسخ حالت ماندگار مدارهای الکتریکی به تحریک های متناوب است. هدف از ارائه این مطلب در وی بدست آوردن نمایش سری فوریه تابع معادله می باشد. دریافت مطلب
