ماتریس ها
الگوریتم ضرب زنجیری ماتریس ها
مساله ضرب زنجیری ماتریسها و پرانتزبندی بهینه آن یکی از مثالهای مشهور کاربرد برنامه نویسی پویا در حل مسائل بهینه سازی است. فرض کنید قصد داریم حاصلضرب عبارت ماتریسی A3 x 7 x B7 x 8 x C8 x 4 را محاسبه کنیم. می دانیم که ضرب ماتریسها خاصیت شرکت پذیری دارند و ترتیب ضرب آنها مهم نیست. پرانتزبندی های مختلف ضرب ماتریس ها حالتهای مختلف محاسبه آن را به ما می دهند: 1: A x ( B x C ) 2: ( A x B ) x C در حالت اول ابتدا B در C ضرب شده و سپس حاصل آنها در A ضرب می شود، و در حالت دوم ابتدا A و B در هم ضرب شده و سپس نتیجه در C ضرب می شود. حال سوال این است که آیا این پرانتزبندی ها تفاوتی با هم دارند؟ ضرب ماتریس دلخواه MR x L در ماتریس دلخواه دیگری مانند NL x C به R x L x C عمل ضرب عددی نیاز دارد (چرا؟). با توجه به این موضوع، تعداد کل عملهای ضرب برای محاسبه حاصلضرب سه ماتریس فوق را در هر دو پرانتزبندی محاسبه می کنیم: 1: A x ( B x C ) : 7 x 8 x 4 + 3 x 7 x 4 = 308 در حالت اول ابتدا ماتریس B در C ضرب می شود. سپس ماتریس A و ماتریس حاصل از ضرب اول، با ابعاد ( ۴ , ۷ )، در هم ضرب می شوند. به همین ترتیب در مورد حالت دوم داریم: 2: ( A x B ) x C : 3 x 7 x 8 + 3 x 8 x 3 = 240 پس در پرانتزبندی به فرم دوم تعداد ضرب کمتری نیاز است. ثابت شده است که تعداد کل حالتهای پرانتزبندی ضرب زنجیری n ماتریس، مطابق با جملات دنباله اعداد کاتالان هستند: هدف ما این است که در بین تمامی این حالت ها، حالتی را بیابیم که حاصل ضرب ماتریسها با حداقل ضرب عددی محاسبه شود. روش تقسیم و حل (Divide and Conquer): ابتدا سعی می کنیم با استفاده از روش تقسیم و حل الگوریتمی برای پاسخ مساله پیدا کنیم. برای اینکار عبارت مورد نظر را به دو قسمت تقسیم می کنیم. به عنوان مثال فرض کنید n = 7 باشد. در این صورت به شش طریق می توان عبارت را به دو دسته تقسیم کرد: 1: ( M1 ) x ( M2 x M3 x M4 x M5 x M6 x M7 ) 2: ( M1 x M2 ) x ( M3 x M4 x M5 x M6 x M7 ) 3: ( M1 x M2 x M3 ) x ( M4 x M5 x M6 x M7 ) 4: ( M1 x M2 x M3 x M4 ) x ( M5 x M6 x M7 ) 5: ( M1 x M2 x M3 x M4 x M5 ) x ( M6 x M7 ) 6: ( M1 x M2 x M3 x M4 x M5 x M6 ) x ( M7 ) هر کدام از حاصلضربهای داخل پرانتزها، زیر مساله ای با n < 7 هستند. همانطور که می دانید در ضرب دو ماتریس، تعداد ستونهای ماتریس اول با تعداد سطرهای ماتریس دوم برابر است. در نتیجه ابعاد هفت ماتریس فوق را به صورت زیر می توان خلاصه کرد: d0 , d1 , d2 , d3 , d4 , d5 , d6 , d7 که ماتریس اول d0 سطر و d1 ستون، ماتریس دوم d1 سطر و d2 ستون، . . . و ماتریس هفتم d6 سطر و d7 ستون دارد. حال تابع Mult را به گونه ای تعریف می کنیم که حداقل ضربهای مورد نیاز برای ضرب ماتریسهای iام تا jام را محاسبه کند. در این صورت برای شش حالت فوق داریم: 1: ( M1 ) x ( M2 x M3 x M4 x M5 x M6 x M7 ) : min1 = Mult( 1, 1 ) + Mult( 2, 7 ) + d0 d1 d7 2: ( M1 x M2 ) x ( M3 x M4 x M5 x M6 x M7 ...
انواع ماتریس ها
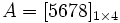
ماتریس مربعی ماتریسی است که تعداد سطرها و ستونهای آن با هم برابر باشد. ماتریس سطری ماتریسی است که یک سطر دارد. مثلا ماتریس ستونی ماتریسی است که یک ستون دارد. مثلا ماتریس ماتریسی است که فقط یک عضو دارد. مثلا ماتریس صفر تمام عضوهای آن ماتریس برابر صفر میباشد. این ماتریس در جمع ماتریسها حکم عدد صفر را در جمع اعداد حقیقی دارد یعنی عضو خنثی است. ماتریس واحد یا یکه ماتریسی است مربعی که عضوهای قطر اصلی آن همگی برابر با یک و بقیه عضوهای آن برابر صفر میباشد. این ماتریس را با I نشان میدهند. مثلا !ماتریس قرینه اگر ماتریسی را در عدد 1- ضرب کنیم قرینه آن ماتریس بدست میآید. بعبارت دیگر قرینه یک ماتریس ، ماتریسی است که عضوهای آن قرینه عضوهای ماتریس اصلی باشند. ماتریس قطری ماتریسی است مربعی که قطر اصلی آن اعداد حقیقی بوده و سایر عضوهای آن برابر صفر باشد. مثلا ماتریس عددی یا اسکالر ماتریسی است قطری که عضوهای قطر اصلی آن برابر باشند. مثلا ماتریس منفرد ماتریسی است مربعی که دترمینان آن برابر صفر باشد. یعنی ماتریس غیرمنفرد یا وارونپذیر اگر در یک ماتریس مربعی دترمینان آن صفر نباشد به آن ماتریس غیرمنفرد میگویند. یعنی ماتریس معکوس یا ماتریس وارون ماتریس مربعی A را در نظر میگیریم اگر ماتریسی مانند B پیدا شود بطوریکه داشته باشیم AB=BA=I به ماتریس B وارون یا معکوس ماتریس A میگویند معمولا ماتریس معکوس A را بصورت نشان میدهند و در نتیجه داریم: ماتریس همسازه اگر در یک ماتریس مربعی به جای هر عضو ، کوفاکتور آن را قرار دهیم ماتریسی بدست میآید که به آن همسازه میگویند. ماتریس همسازه A را با N نمایش میدهند.برای هر در ماتریس ، همسازه برابر است با عدد کوفاکتور عضو بطوریکه ، را دترمینان ماتریس حاصل از حذف سطر i ام و ستون j ام ماتریس A میتوان تعریف کرد. ماتریس وابسته یا الحاقی به ترانسپوزه ماتریس همسازه A ماتریس وابسته A میگویند و آن را با نشان میدهند. ماتریس متقارن اگر ترانسپوزه یک ماتریس با آن ماتریس برابر باشد آن ماتریس را متقارن مینامند بعبارت دیگر ماتریس A متقارن است در صورتیکه باشد. اگر در ماتریس جای سطرها و ستونها را عوض کنیم و ماتریس تغییر نکند به آن متقارن میگویند.
تعریف ماتریس ها
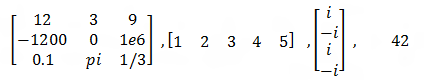
موضوع اساسی که برنامه متلب به آن می پردازد یک ماتریس است . یک ماتریس آرایه ای از اعداد است. به عنوان مثال آرایه های عددی زیر ماتریس هستند: اندازه ماتریس، تعداد سطرها در تعداد ستون ها است. ماتریس اولی یک ماتریس ۳×۳ است. عنصر (۳,۲) (سطر سوم در ستون دوم) آن عدد pi=3.14159 و در عنصر (۲,۳) (سطر دوم در ستون سوم) آن عدد 1e6 (یک میلیون) که مخفف 1x106 می باشد. ماتریس دوم یک ماتریس ردیف برداری و ماتریس سوم یک ماتریس ستون برداری که شامل عدد i که ریشه دوم عدد 1- می باشد و در برنامه متلب از پیش تعریف شده است. ماتریس آخری یک ماتریس 1×1 است که آن را یک اسکالر می نامند. -----------------------------------
ماتریسها
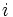
در ریاضیات ماتریس عبارت است یک جدول مستطیلی از اعداد و یا به صورت ساخت یافتهتر: ماتریس مجموعهای از اشیای هم نوع است که به تعدادی گروه با اعضای یکسان تقسیم بندی شده است. ماتریسها ریاضیات مناسبی برای ثبت و ذخیره دادههایی هستند که مقادیر آنها به دو کمیت بستگی دارد. از این جهت چون در اکثر علوم با چنین دادههایی روبرو میشویم. بنابراین کاربرد وسیع ماتریسها در اکثر شاخههای علوم مهندسی میشود. ماتریس ماتریس عبارت است از آرایشی (آرایهای) مستطیل شکل از اعداد مختلط به طوری که عناصر این آرایه را درایه مینامیم و عنصر واقع در سطر ام و ستون ام را با نماد نشان میدهیم. ماتریسی که دارای سطر و ستون باشد را ماتریس از مرتبه در مینامیم.( ) نکته هرگاه آنگاه ماتریس را مربع از مرتبه مینامیم. یک ماتریس را بصورت نمایش میدهیم. تاریخچه مطالعه روی انواع خاصی از ماتریسها مانند مربعهای جادویی و مربعهای لاتین ، به تاریخ قبل از میلاد نسبت داده شده است. معرفی و تکامل نمایش ماتریسها به عنوان شاخهای از جبر خطی در نتیجه مطلعه روی ضرایب سیستم معادلات خطی و الگوها و روشهای حل آنها بوجود آمد. لایب نیتس به عنوان یکی از پایه گذاران علم حسابان در سال 1693، دترمینان ماتریسها را معرفی کرد. در ادامه کرامر روش خود را برای حل دستگاه معادلات خطی بر اساس دترمینان ماتریس ضرایب دستگاه معرفی کرد. این روش که به روش کرامر مرسوم است، بر اساس استفاده صریح از دترمینان ماتریس ضرایب معرفی گردیده است. در مقابل اولین استفاده ضمنی از ماتریسها توسط لاگرانژ برای تعیین ماکزیمم و مینیمم توابع چند مقداری مورد استفاده قرار گرفت. در ادامه گاوس روش حذفی خود را برای حل مسائل کمترین مربعات که کاربردهای بسیار وسیعی در علوم سماوی و ژئودوزی دارد را معرفی کرد. روابط بین ماتریسها تساوی دو ماتریس دو ماتریس و مساوی اند اگر و فقط اگر (هم مرتبه باشند) و جمع دو ماتریس اگر و آنگاه قرینه ماتریس اگر آنگاه قرینه را بصورت زیر تعریف میکنیم: ضرب اسکالر در ماتریس اگر و یک اسکالر باشد آنگاهدر ضرب اسکالر یک عدد در یک ماتریس ضرب میشود. در این نوع ضرب تمامی عناصر ماتریس در آن عدد ضرب میشوند به عنوان مثال: و نمایش ریاضی آن به صورت زیر می باشد: cA)ij = c(A)ij) ضرب ماتریسها اگر و آنگاه ضرب دو ماتریس را با علامت نمایش داده و بصورت زیر تعریف خواهیم کرد: در این نوع هر دو ضرب شونده و ضرب کننده از نوع ماتریس میباشند. بطور مشابه ضرب دو ماتریس نیز باید یک جنبه خوش تعریفی داشته باشد. ضرب دو ماتریس داده شده A و B زمانی خوش تعریف است که تعداد ستونهای ماتریس ضرب کننده با ...
محاسبه ماتریس ها

ماتریس ها را می توان جمع یا تفریق کرد. (فقط در صورتی که اندازه ماتریس ها یکسان است. )<?xml:namespace prefix = o ns = "urn:schemas-microsoft-com:office:office" /> >> a=[1 2 3; 4 5 6; 7 8 9] a = 1 2 3 4 5 6 7 8 9 >> b=10*a b = 10 20 30 40 50 60 70 80 90 >> c=a+b c = 11 22 33 44 55 66 77 88 99 >> c-b ans = 1 2 3 4 5 6 7 8 9 -----------------------------------
ماتریس
کاربرد در شبیه سازی، پردازش تصویر، و ترافیک و سازه های شهری، حل معادلات طولانی ***************************************در تاریخ آمده است.که اولین بار بک ریاضیدان انگلیسی تبار بنام کیلی ماتریس را در ریاضیات وارد کرد.با توجه به آنکه در آن زمان ریاضیدانان اغلب به دنبال مسائل کاربردی بودند کسی توجهی به آن نکرد.اما بعدها ریاضیدانان دنباله ی کار را گرفتند تا به امروز رسید که بدون اغراق می توان گفت در هر علمی به گونه ای با ماتریس سروکار دارند.یکی از نقش های اصلی ماتریس ها آن است که آنها ابزار اصلی محاسبات عملی ریاضیات امروزی هستند.درست همان نقشی که سایقا اعداد بر عهده داشتند. از این نظر می توان گفت نقش امروز ماتریس ها همان نقش دیروز اعداد است.البته ماتریس ها به معنایی اعداد و بردارها را در بردارند..بنابراین می توان آنها را تعمیمی از اعداد و بردارها در نظر گرفت.در ریاضیات کاربردی ماتریس ها از ابزار روزمره هستند.زیرا ماتریسها با حل دستگاه معادلات خطی ارتباط تنگاتنگی دارند و برای حل ریاضی مسائل عملی مناسب ترین تکنیک فرمول بندی مسئله و یا تقریب زدن جوابهای مسئله با دستگاه معادلات خطی است که در نتیجه ماتریس ها وارد کار می شوند. از جنبه ی نظری فیزیک امروزی که فیزیک کوانتوم است بدون ماتریس ها نمی توانست بوجود آید.هایزنبرگ – اولین کسی که در فیزیک مفاهیم ماتریسها را به کار برد- اعلام کرد."تنها ابزار ریاضی من در مکانیک کوانتوم به آن احتیاج دارم ماتریس است".بسیاری از جیرهایی که تا به حال دیده اید مانند جبر اعداد مخنلط و جبر بردارها را با ماتریسها بسیار ساده می توان بیان کرد.*************************************ماتریسماتریس عبارت است از آرایشی (آرایهای) مستطیل شکل از اعداد مختلط به طوری که عناصر این آرایه را درایه مینامیم و عنصر واقع در سطر ام و ستون ام را با نماد نشان میدهیم. ماتریسی که دارای سطر و ستون باشد را ماتریس از مرتبه در مینامیم.( )نکتههرگاه آنگاه ماتریس را مربع از مرتبه مینامیم. یک ماتریس را بصورت نمایش میدهیم.تاریخچهمطالعه روی انواع خاصی از ماتریسها مانند مربعهای جادویی و مربعهای لاتین ، به تاریخ قبل از میلاد نسبت داده شده است. معرفی و تکامل نمایش ماتریسها به عنوان شاخهای از جبر خطی در نتیجه مطلعه روی ضرایب سیستم معادلات خطی و الگوها و روشهای حل آنها بوجود آمد. لایب نیتس به عنوان یکی از پایه گذاران علم حسابان در سال 1693، دترمینان ماتریسها را معرفی کرد. در ادامه کرامر روش خود را برای حل دستگاه معادلات خطی بر اساس دترمینان ماتریس ضرایب دستگاه معرفی کرد. این روش که به روش کرامر مرسوم است، بر ...
ماتریس ها
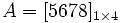
ماتریسی است که یک سطر دارد. مثلا ماتریس ستونی ماتریسی است که یک ستون دارد. مثلا ماتریس ماتریسی است که فقط یک عضو دارد. مثلا ماتریس صفر تمام عضوهای آن ماتریس برابر صفر میباشد. این ماتریس در جمع ماتریسها حکم عدد صفر را در جمع اعداد حقیقی دارد یعنی عضو خنثی است. ماتریس واحد یا یکه ماتریسی است مربعی که عضوهای قطر اصلی آن همگی برابر با یک و بقیه عضوهای آن برابر صفر میباشد. این ماتریس را با I نشان میدهند. مثلا !ماتریس قرینه اگر ماتریسی را در عدد 1- ضرب کنیم قرینه آن ماتریس بدست میآید. بعبارت دیگر قرینه یک ماتریس ، ماتریسی است که عضوهای آن قرینه عضوهای ماتریس اصلی باشند. ماتریس قطری ماتریسی است مربعی که قطر اصلی آن اعداد حقیقی بوده و سایر عضوهای آن برابر صفر باشد. مثلا ماتریس عددی یا اسکالر ماتریسی است قطری که عضوهای قطر اصلی آن برابر باشند. مثلا ماتریس منفرد ماتریسی است مربعی که دترمینان آن برابر صفر باشد. یعنی ماتریس غیرمنفرد یا وارونپذیر اگر در یک ماتریس مربعی دترمینان آن صفر نباشد به آن ماتریس غیرمنفرد میگویند. یعنی ماتریس معکوس یا ماتریس وارون ماتریس مربعی A را در نظر میگیریم اگر ماتریسی مانند B پیدا شود بطوریکه داشته باشیم AB=BA=I به ماتریس B وارون یا معکوس ماتریس A میگویند معمولا ماتریس معکوس A را بصورت نشان میدهند و در نتیجه داریم: ماتریس همسازه اگر در یک ماتریس مربعی به جای هر عضو ، کوفاکتور آن را قرار دهیم ماتریسی بدست میآید که به آن همسازه میگویند. ماتریس همسازه A را با N نمایش میدهند.برای هر در ماتریس ، همسازه برابر است با عدد کوفاکتور عضو بطوریکه ، را دترمینان ماتریس حاصل از حذف سطر i ام و ستون j ام ماتریس A میتوان تعریف کرد. ماتریس وابسته یا الحاقی به ترانسپوزه ماتریس همسازه A ماتریس وابسته A میگویند و آن را با نشان میدهند. ماتریس متقارن اگر ترانسپوزه یک ماتریس با آن ماتریس برابر باشد آن ماتریس را متقارن مینامند بعبارت دیگر ماتریس A متقارن است در صورتیکه باشد. اگر در ماتریس جای سطرها و ستونها را عوض کنیم و ماتریس تغییر نکند به آن متقارن میگویند. ماتریس ضدمتقارن یا آنتیمتقارن هرگاه قرینه ترانسپوزه ماتریس A برابر A شود، به آن ماتریس ضدمتقارن میگویند و داریم ماتریس پایین مثلثی اگر در یک ماتریس مربعی تمام عضوهای بالای قطر اصلی صفر باشند به آن ماتریس پایین مثلثی میگویند یعنی ماتریس بالا مثلثی اگر در یک ماتریس مربعی تمام عضوهای پایین قطر اصلی صفر باشند به آن ماتریس بالا مثلثی میگویند. یعنیماتریس متعامد اگر در ماتریس مربعی A داشته باشیم به ماتریس متعامد میگویند ...
مبحث ماتریس
ماتریس ماتریس به یک آرایش منظم از اعداد گفته میشود. به طوری که میتوان گفت که هر ستون یا هر سطر یک ماتریس، یک بردار را تشکیل میدهد. در جبر خطی، میتوان اثبات کرد که هر نگاشت خطیِ، از فضای به فضای ، هم ارز (isomorph) با یک ماتریس (m سطر و n ستون) میباشد. ماتریسها کاربردهای فراوانی در جبر خطی دارند. از جمله در انتقالهای خطی و در حل دستگاه معادلات خطی. ماتریسها میتوانند که با همدیگر جمع، از هم تفریق، در هم ضرب یا... (با قوانین خودشان) بشوند. اگر دترمینان یک ماتریس مربعی نا صفر باشد، آنگاه آن ماتریس را ماتریس معکوسپذیر نامند.درایهها به هر یک از عناصر موجود در یک ماتریس درایه میگویند. برای مشخص کردن هر درایه باید نام ردیف و ستون را در پایین نام ماتریس نوشت. برای مثال اگر نام ماتریسی i باشد درایهای که در ردیف اول و ستون دوم قرار دارد به این صورت نشان داده میشود: i1,2 انواع ماتریس ها-قرینه ماتریسMay 30, 2010 | admin آموزش ریاضیات:انواع ماتریس ها ماتریس قطری چیست؟ تعریف ماتریس قطری:ماتریس مربع A را قطری می نامیم هرگاه,درایه های طرفین قطر اصلی آن صفر باشد.برای مثال ماتریس یک ماتریس قطری است. ماتریس همانی چیست؟ تعریف ماتریس همانی:ماتریس مربعی را که درایه های قطر اصلی آن یک و سایر درایه های آن صفر باشد را ماتریس همانی (واحد) می نامیم و آن را با In یا Iنمایش می دهیم. ماتریس های مساوی: دو ماتریس را مساوی می گوییم هرگاه درایه های آن ها نظیر به نظیر باهم برابر باشند. ماتریس های هم مرتبه: دو ماتریس را که تعداد سطر ها و ستون های آن ها با هم برابر باشند ماتریس های هم مرتبه می گویند. نکته ای که از این تعریف می توان نتیجه گرفت اینست که اگر دو ماتریس هم مرتبه نباشند,با هم مساوی نیستند. ماتریس صفر: هرگاه تمام درایه های یک ماتریس صفر باشد,آن را ماتریس صفر می نامند و با نماد نمایش می دهند. تعریف قرینه ی ماتریس : قرینه ماتریس A از قرینه کردن تک تک درایه های ماتریس A بدست می آید.قرینه ی ماتریس A را به صورت A- نمایش می دهیم.ماتریس اسکالر ماتریس قطری که تمام درایههای قطر اصلی ان برابر باشد یک ماتریس اسکالر نامیده میشود و برابر با همان مقدار درایه در ضرب ماتریسهاست یا به عبارت دیگر λIکه I ماتریس همانی است. برای مثال ماتریس ۳×۳ اسکالر به این شکل است: رای پیدا کردن معکوس ماتریس 3 در 3 ، ابتدا دترمینان آن را حساب می کنیم.اگر دترمینان مساویصفر باشد ، ماتریس معکوس وجود ندارد. محاسبه دترمینان ماتریس 3 در 3 اگر ماتریس A را بصورت زیر در نظر بگیریم : برای محاسبه دترمینان ماتریس A خواهیم ...
121- ماتریس هدف ها(OMAX)
کتاب Tool Navigator ترجمه : مدینه شیری [email protected] تعریف ابزاری: ماتریس هف ها(OMAX) یک فرم گزارشی قدرت مند است که اجازه نظارت بر سرعت اجرای همه ی هدف های بیان شده در داخل حوزه ی مدیریت پروژه را می دهد. که در ابتدا توسط Felix, Riggs در سال 1983 معرفی شد و توسط S.L.Dockstader در سال 1987 اجرا شد.این ابزار می تواند به عنوان یک سند علمی برای گزارش یک وضعیت کار کند و یک مکانیسم امتیاز بندی و اندازه گیری را در هر زمانی،در عملکرد کلی ارائه می دهد. کاربرد نوعی (نمونه): برای پیگیری عملکرد سازمان در مقابل یک مجموعه ای از هدف های تغییر. برای سنجش پیشرفت انجام شده و ارائه ی یک فهرستی مرکب از پیشرفت ها و دست یابی های نمایی. برای ارائه ی یک گزارش از وضعیت شرح داده شده از پیشرفت انجام شده برای مدیریت ارشد. مرحله ی حل مشکل: انتخاب و تعریف مشکل یا فرصت تشخیص و تحلیل علل یا تغییر عامل بالقوه برنامه ریزی وطرح ریزی راه حل های ممکن یا تغییر به کار گیری وارزیابی راه حل یا تغییر سنجش وگزارش راه حل یا نتایج تغییر تشخیص(شناخت) واعطای پاداش به تلا ش های تیمی یادداشت ها و نکات کلیدی: امتیازهای 1تا15منعکس کننده ی پیشرفت در اجرای هدف هاست .در مثال نشان داده شده ،هدف2 ،"اداره کردن100جلسه ی راهنمایی (آشنا یی) 45 درصد کامل شده است(عملکرد جاری راببینید.) این برابراست با یک امتیاز5/4 (امتیازرادرستون2ببینید.)که با ضرب کردن دروزن5 به ارزش 5/22رسیده است. فرکانس(فراوانی)اندازه گیری توسط صاحبان فرآیند مدیریت ارشدتعیین میشود. فرآیند مرحله به مرحله: مرحله ی 1: اولین مرحله مستلزم پیشرفت وتوسعه ی هدف های قابل اندازه گیری است برای اینکه در فرم OMAX (ماتریس هدف ها ) درج شود. مثال"هدف عمومی-" تأسیس تیم های IPD " رامشاهده کنید.(مراجعه کنیدبه مثالی در جدول ماتریس هدف ها محاسبات ومراحل) مرحله ی 2: تیم شمارنده ها را برای هر ستون هدف توسعه می دهد.مثال" تأسیس 20تیم IPD "از صفرتا20خواهدبودبرای امتیاز از0تا10. مرحله ی3: تیم،وزن یا اهمیت هر هدف را در نظر می گیرد و توانق عام رادرضریب تغییر وزن برای اینکه بتواند به همه ی هدف ها اختصاص دهد بدست می آ ورد،همان طور که درمثال نشان داده شده است.(وزن را مشاهده کنید ).دقت کنید که مجموع ردیف وزن باید برابر100شود. مرحله ی4: هرگاه یک سنجش عملکرد مورد نیازاست،ردیف عملکرد جاری(تکمیل شده)با داده ها ی واقعی پر می شود. مرحله ی5: امتیازات مربوطه،شناخته شده و در ردیف امتیاز،درج می شوند.مثال:امتیاز 2 به 4 در ستون 1 مربوط می شود،که همچنین عملکرد جاری(تکمیل شده) 4 تیم IPD تأسیس شده را منعکس می کند. کتاب Tool Navigator
