سری فوریه (تکمیلی)
برای تابع متناوب 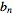 در یک بازه مثل
در یک بازه مثل  به جای
به جای  ، یک تغییر ساده ی متغیرها می تواند برای تبدیل بازه ی انتگرالگیری از
، یک تغییر ساده ی متغیرها می تواند برای تبدیل بازه ی انتگرالگیری از ![[-pi,pi]](http://www.bargozideha.com/static/portal/83/836424-591299.gif) به
به ![[-L,L]](http://www.bargozideha.com/static/portal/96/968270-204560.gif) مورد استفاده قرار بگیرد. فرض کنیم:
مورد استفاده قرار بگیرد. فرض کنیم:

با حل معادله اول نسبت به  داریم
داریم  ، لذا با وارد کردن این به
، لذا با وارد کردن این به
خواهیم داشت:
بنابراین:
به طور یکسان، برای تابعی که در بازه ی ![[0,2L]](http://www.bargozideha.com/static/portal/42/420526-753828.gif) تعریف می شود، معادلات بالا به سادگی به اشکال زیر تبدیل می شوند:
تعریف می شود، معادلات بالا به سادگی به اشکال زیر تبدیل می شوند:
   |
   |
   |
در حقیقت برای تابع متناوب  با دوره ی
با دوره ی  ، هر بازه ی
، هر بازه ی  با توجه به یکی از دو اصل راحتی یا اولویت شخصی می تواند بکار گرفته شود (Arfken 1985, p. 769).
با توجه به یکی از دو اصل راحتی یا اولویت شخصی می تواند بکار گرفته شود (Arfken 1985, p. 769).
ضرایب (coefficients) برای بسط های سری های فوریه ی تعدادی از توابع مرسوم در Beyer, 1987, pp. 411-412 و Byerly, 1959, p. 51 آمده است. یکی از مرسوم ترین توابعی که با استفاده از تکنیک اخیر مورد تجزیه تحلیل قرار می گیرد، موج چهار گوش یا مربعی (square wave) است. سری های فوریه برای تعدادی از توابع مرسوم در جدول زیر گرداوری شده اند.
|
تابع |
سری فوریه | |
اگر یک تابع زوج باشد، یعنی  ، آنگاه
، آنگاه  زوج است. (این بدان خاطر است که چون
زوج است. (این بدان خاطر است که چون  فرد است و یک تابع زوج (even function) ضرب در یک تابع زوج برابر با یک تابع فرد (odd function) است.) بنابراین برای تمامی nها
فرد است و یک تابع زوج (even function) ضرب در یک تابع زوج برابر با یک تابع فرد (odd function) است.) بنابراین برای تمامی nها  . به طور یکسان، اگر یک تابع فرد است، پس
. به طور یکسان، اگر یک تابع فرد است، پس  ، آنگاه
، آنگاه  فرد است. (این بدان خاطر است که چون
فرد است. (این بدان خاطر است که چون  زوج است و یک تابع زوج (even function) ضرب در یک تابع فرد برابر با یک تابع فرد (odd function) است.) بنابراین برای تمامی nها
زوج است و یک تابع زوج (even function) ضرب در یک تابع فرد برابر با یک تابع فرد (odd function) است.) بنابراین برای تمامی nها 
نظریه ی سری های فوریه همچنین می تواند به ضرایب مختلط (complex coefficients) بسط داده شود. یک تابع حقیقی-مقدار را در نظر می گیریم. می نویسیم:
حال بررسی می کنیم که
   |
  |
![sum_(n=-infty)^(infty)A_nint_(-pi)^pi{cos[(n-m)x]+isin[(n-m)x]}dx](http://www.bargozideha.com/static/portal/43/430534-559492.gif)  |
  |
  |
لذا
ضرایب (coefficients) را می توان برحسب آنهایی که در سری های فوریه گفته شده اند، توضیح داد:![1/(2pi)int_(-pi)^pif(x)[cos(nx)-isin(nx)]dx](http://www.bargozideha.com/static/portal/97/971441-651560.gif)   |
![{1/(2pi)int_(-pi)^pif(x)[cos(nx)+isin(nx)]dx n<0; 1/(2pi)int_(-pi)^pif(x)dx n=0; 1/(2pi)int_(-pi)^pif(x)[cos(nx)-isin(nx)]dx n>0](http://www.bargozideha.com/static/portal/98/988510-544041.gif)  |
  |
برای یک تابع متناوب در ![[-L/2,L/2]](http://www.bargozideha.com/static/portal/51/514329-650839.gif) ، اینها به شکل های زیر تبدیل خواهند شد:
، اینها به شکل های زیر تبدیل خواهند شد:
   |
   |
این معادلات مبنای مهمی برای شکل گیری تبدیل فوریه (Fourier transform) محسوب می شوند که با تبدیل  از یک متغیر مجزا به یک متغیر پیوسته در طول
از یک متغیر مجزا به یک متغیر پیوسته در طول  بدست می آید.
بدست می آید.
لینک مربوطه: سری فوریه
منابع:
Arfken, G. "Fourier Series." Ch. 14 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 760-793, 1985.
Askey, R. and Haimo, D. T. "Similarities between Fourier and Power Series." Amer. Math. Monthly 103, 297-304, 1996.
Beyer, W. H. (Ed.). CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, 1987.
Brown, J. W. and Churchill, R. V. Fourier Series and Boundary Value Problems, 5th ed. New York: McGraw-Hill, 1993.
Byerly, W. E. An Elementary Treatise on Fourier's Series, and Spherical, Cylindrical, and Ellipsoidal Harmonics, with Applications to Problems in Mathematical Physics. New York: Dover, 1959.
Carslaw, H. S. Introduction to the Theory of Fourier's Series and Integrals, 3rd ed., rev. and enl. New York: Dover, 1950.
Davis, H. F. Fourier Series and Orthogonal Functions. New York: Dover, 1963.
Dym, H. and McKean, H. P. Fourier Series and Integrals. New York: Academic Press, 1972.
Folland, G. B. Fourier Analysis and Its Applications. Pacific Grove, CA: Brooks/Cole, 1992.
Groemer, H. Geometric Applications of Fourier Series and Spherical Harmonics. New York: Cambridge University Press, 1996.
Körner, T. W. Fourier Analysis. Cambridge, England: Cambridge University Press, 1988.
Körner, T. W. Exercises for Fourier Analysis. New York: Cambridge University Press, 1993.
Krantz, S. G. "Fourier Series." §15.1 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 195-202, 1999.
Lighthill, M. J. Introduction to Fourier Analysis and Generalised Functions. Cambridge, England: Cambridge University Press, 1958.
Morrison, N. Introduction to Fourier Analysis. New York: Wiley, 1994.
Sansone, G. "Expansions in Fourier Series." Ch. 2 in Orthogonal Functions, rev. English ed. New York: Dover, pp. 39-168, 1991.
Weisstein, E. W. "Books about Fourier Transforms." http://www.ericweisstein.com/encyclopedias/books/FourierTransforms.html.
Whittaker, E. T. and Robinson, G. "Practical Fourier Analysis." Ch. 10 in The Calculus of Observations: A Treatise on Numerical Mathematics, 4th ed. New York: Dover, pp. 260-284, 1967
مطالب مشابه :
تبدیل فوریه
matlab - تبدیل فوریه - یک قضیه ریاضی می گوید که تقریبا همه توابع را می توان به عنوان مجموعه ای
تبدیلات فوریه (1)
تبدیل فوریه را می توان همواره به صورت جملاتی از تبدیل cos فوریه (Fourier cosine transform)
تبدیل فوریه
همانطور که می دانید مهمترین ویژگی در ادای هر حرف فرکانس های تشکیل دهنده آن حرف می باشد.
تبدیل فوریه
مهندسی برق - تبدیل فوریه - سری فوریه، روشی در ریاضیات میباشد که به وسیله آن، هر تابع
تبدیل فوریه
تبدیل فوریه گسسته مختلط سیگنال s به طول N را می توان با استفاده از رابطه زیر تعریف کرد:
تبدیل فوریه
math world (جهان ریاضی) - تبدیل فوریه - دادمنش تبدیل فوریه، نامیده شده به اسم ریاضیدان ِ فرانسوی
تبدیلات فوریه (2)
که تابع دلتای دیراک (Delta Function) است. تعجب آور است که خودهمبستگی به سادگی توسط تبدیل فوریه ی
تبدیل فوریه
تبدیل فوریه، نامیده شده به اسم ریاضیدانِ فرانسوی ژوزف فوریه، یک تبدیل انتگرالی است که هر
تبدیل فوریه
بهترین های برق شیخ بهایی - تقدیم به آنان که نمیدانیم در یادشان خواهیم ماند یا برایشان خاطره
طیف سنجی مادون
طیف سنجی مادون قرمز ، روشی برای شناسایی مولکولها و بخصوص گروه عاملی مولکولهاست. هر مادهای
برچسب :
تبدیل فوریه




















![2[H(x/L)-H(x/L-1)]-1](http://www.bargozideha.com/static/portal/21/218089-226867.gif)




