بسط تیلور
بسط و سری
بسط تیلور از ویکیپدیا، دانشنامهٔ آزاد پرش به: ناوبری, جستجو sinx و بسط تیلور آن، تا توانهای 1, 3, 5, 7, 9, 11 و 13. به وسیلهٔ بسط تیلور، میتوان توابع بینهایت بار مشتقپذیر را به صورت توابع توانی نوشت، و یا به عبارتی، بسط داد. تعریف: اگر f در همسایگی x0 و بینهایت بار مشتقپذیر باشد،آنگاه f را میتوان به صورت توانهایی از (x − x0) نوشت. که در اینجا، fn(x) مشتق n-اُم تابع f است. این بسط به نام ریاضیدانانگلیسیبروک تیلور اسمگذاری شده است. متاسفانه، این بسط برای همهٔ توابع حقیقی انجامپذیر نیست. مثال: f(x) = e2x در همسایگی 1- بینهایت بار مشتقپذیر است. میتوان گفت: همچنین، از بسط تیلور میتوان برای حل از روش سریهای توانی استفاده کرد . حالت خاص سری تیلور که در حول نقطه 0 میباشد را سری مکلورن میگویند. تابع تحلیلی از ویکیپدیا، دانشنامهٔ آزاد پرش به: ناوبری, جستجو در ریاضیات یک تابع تحلیلی، تابعی است که به طور محلی به وسیله یک سری توانی همگرا مشخص می شود. می توان به توایع تحلیلی مانند یک پل بین چند جمله ایها و توابع در حالت کلی فکر کرد. اینجا توابع تحلیلی حقیقی و توابع تحلیلی مختلط وجود دارند، که شباهتها و تفاوتهایی دارند. یک تابع تحلیلی است اگر برابر با سری تیلورش در یک همسایگی باشد. تعاریف تابع f رو مجموعهٔ باز D در خط حقیقی، تحلیلی حقیقی است اگر برای هر x0 در D بتوان نوشت: در این فرمول ضرایب a0, a1, ... اعداد حقیقی هستند و سری برای x در یک همسایگی از x0 همگرا است. به صورت دیگر، یک تابع تحلیلی یک تابع بینهایت بار مشتق پذیراست به این صورت که سری تیلور در هر نقطه x0 در دامنه اش برای x به اندازه کافی نزدیک به x0 همگراست و مقدارش برابر با f(x) است. تعریف یک تابع تحلیلی مختلط با جایگزین کردن «مختلط» به جای «حقیقی» و «صفحهٔ مختلط» به جای «خط حقیقی» در مطالب بالا بدست می آید. مثال ها هر چند جملهای (حقیقی یا مختلط) یک تایع تحلیلی است. به این دلیل که اگر یک چند جمله ای از درجه n باشد، هر جمله ازدرجه بزرگتر از n در بسط سری تیلورش صفر است، وبنا براین، این سری به طور جزئی همگرا خواهد بود. تابع نمایی تحلیلی است. هر سری تیلور برای این تابع نه فقط برای x به اندازه کافی نزدیک به x0 (همان طور که در تعریف آمده) بلکه برای همه مقدار x (حقیقی یا مختلط) همگرا می شود. توابع مثلثاتی، لگاریتم و توابع توانی روی هر بازهٔ باز در دامنهٔشان تحلیلی اند. تابع قدر مطلق تحلیلی نیست زیرا مشتق پذیر نیست. توابع تعریف شدهٔ تکه ای(تابعهای معلوم به وسیله فرمولهای مختلف در مناطق مختلف) تحلیلی نیستند. خصوصیات توابع تحلیلی مجموع ها، ضرب ها و ترکیبات توابع تحلیلی، تحلیلی ...
بسط تیلور
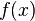
در ریاضیات، سری تیلور یا گسترش تیلور (به انگلیسی: Taylor series) نمایش یک تابع به صورت مجموع بی نهایت جمله است که از مشتقهای تابع در یک نقطه به دست میآید. ریاضیدان انگلیسی، بروک تیلور، در سال ۱۷۱۵ میلادی، مفهوم سری تیلور را به طور رسمی معرفی کرد. اگر سری را دور نقطه صفر گسترش دهیم، سری به سری مکلارن نیز معروف است که به نام ریاضیدان اسکاتلندی، کالین مکلارن، که در قرن 18ام استفاده بسیاری از این حالت خاص سری تیلور کرد، نام گزاری شده است. مرسوم است که توابع را حول یک نقطه با تعدادی متناهی از جملات سری تیلور تقریب بزنند. قضیه تیلور مقدار خطای این تقریب زنی را به صورت کمّی تخمین میزند. هر تعداد متناهی از جملات اول سری تیلور به چندجملهای تیلور معروف است. سری تیلور یک تابع، حد چندجملهای های تیلور آن است (اگر حد وجود داشته باشد.) یک تابع ممکن است با سری تیلورش برابر نباشد حتی اگر سری تیلور آن در هر نقطه همگرا باشد. تابعی که در یک بازهی باز (یا یک دیسک در صفحه مختلط) با سری تیلورش برابر باشد، تابع تحلیلی خوانده میشود.تعریف سری تیلور یک تابع با مقادیر حقیقی یا مختلط که در همسایگی نقطه حقیقی یا مختلط بی نهایت بار مشتقپذیر است، سری توانیِ زیر است:که میتوانیم آن را خلاصهتر عملگر سیگما بنویسیم:که در اینجا به معنی فاکتوریل عدد و به معنی مشتق اُم تابع در نقطه است. طبق تعریف مشتق 0-اُم هر تابع خودش است و و هر دو برابر 1 اند. اگر باشد، سری همان سری مکلورن است. هر چه درجه چند جمله ای تیلور افزایش پیدا کند، دور نقطه گسترش، تابع تقریب تیلور به تابع اصلی نزدیکتر میشود. این تصویر و تقریب های تیلور آن، تا توانهای 1, 3, 5, 7, 9, 11 و 13 را نشان میدهد.اثبات : فرض کنید میخواهیم تابعی چندجملهای مثل مدلسازی کنیم که در همسایگی نقطه با تابع یکریخت باشد. اول اینکه باید مقدار تابع در نقطه با برابر باشد پس داریم: تا اینجا داریم و اکنون برای اینکه تابع در همسایگی نیز شبیه شود باید مشتقهای آن در این نقطه با مشتقهای برابر باشد. مشتقهای را به صورت مضاربی از x به اضافه میکنیم به طوری که: (1) در نقطهی برابر صفر باشند تا مدل به هم نخورد و (2) مشتق i-اُمِ برابر با مشتق i-اُمِ باشد. برای برقراری شرط یک و دو کافیست مقدار عددی مشتق i-اُمِ را به ضریبِ قرار دهیم. در این صورت این مقدار تا مشتق i-اُم صفر باقی خواهد ماند و چون در هر مشتق این مقدار در توانِ صورت ضرب میشود هنگامِ گرفتن مشتق i-اُم خواهیم داشت . اگر اضافه کردن مشتقات را تا ابد ادامه دهیم تابع بیشتر شبیه شده تا در بینهایت همارز خود شود.یا همان:گاهی در گرفتن حد، از یک یا ...
بسط تیلور سینوس و کسینوس
program donbale integer ::i,j,d,t,e real::x,a,b,f,fact,k,m,h,g,z print*,"x ra vared konid" read*,x a=1 do i=4,10000,step4 a = a + (x**i)/fact(i) end do b=0 do j=2,10000,step4 b=b+(x**j)/fact(j) end do f = a - b print*," cos(x)= " print*,f g=0 do e=1,10000,step4 g=g+(x**e)/fact(e) end do h=0 do t=3,10000,step4 h=h+(x**t)/fact (t) end do z = g – h print*,"sin(x) =" print*,z end program function fact(k) integer::k,fact,m,d m=1 do d=1,k m=m*d end do print*,m end function
سری فوریه و تیلور

ژوزف فوریهژان باپتیست ژوزف فوریه متولد ۲۱ مارس ۱۷۶۸اوسر , فرانسه مرگ ۱۶ مه ۱۸۳۰پاریس , فرانسه رشته فعالیت ریاضیات, فیزیک و تاریخ استاد راهنما ژوزف لویی لاگرانژ دلیل شهرت سری فوریهتبدیل فوریهآنالیز فوریه ژان باپتیست ژوزف فوریه (به فرانسوی: Joseph Fourier) (متولد ۲۱ مارس ۱۷۶۸ در اوسر؛ درگذشتهٔ ۱۶ مه ۱۸۳۰ در پاریس)، ریاضیدان و فیزیکدان فرانسوی. پدر فوریه به خیاطی اشتغال داشت و زمانی که وی هشت سال بیشتر نداشت، از دنیا رفت. فوریه در مدرسه نظامیِ زادگاهاش شروع به تحصیل کرد. او در ۱۸ سالگیش در همین دانشگاه به تدریس ریاضی مشغول شد و با به وقوع پیوستن انقلاب فرانسه از آن حمایت کرد. در دوران ترور مدتی به زندان افتاد، اما بعدا در سال ۱۷۹۵ آزاد شد و به استخدام اکول نرمال سوپریور درآمد. وی از سال ۱۷۹۷ به عنوان جانشین لاگرانژ در اکول پلیتکنیک به تدریس مشغول شد. فوریه اواخر قرن هجدهم، ناپلئون بناپارت را در لشکرکشی به مصر همراهی میکرد . وی در مصر به عنوان فرماندار مصر سفلی و نیز دبیر بنیاد مصرشناسی مشغول بود. پس از بازگشت فوریه از مصر، در سال ۱۸۰۱ او به عنوان فرماندار ایزر (Isère) منصوب شد و در سال ۱۸۰۸ به لقب بارون دست یافت. از سال ۱۸۲۲ و تا پایان عمرش در سمت دبیر دائمی فرهنگستان علوم فرانسه قرار داشت. فوریه در زمینه فیزیک بر روی انتقال گرما تحقیق میکرد و قانون فوریه در این زمینه از او به جای ماندهاست. فوریه همچنین کاربردهای سری فوریه در زمینه انتقال گرما و نیز ارتعاشات را معرفی کرد. فوریه در سال ۱۸۳۰ و در ۶۲سالگی از دنیا رفت. جسد وی در گورستان پر-لاشز دفن شده است. فوریه یکی از ۷۲ نفر فرانسوی است که نام آنها بر روی برج ایفل حک شده است.سری فوریهتبدیل فوریه در ریاضیات، سری فوریه، تابعی است که با استفاده از آن می توان هر تابع متناوب را به صورت جمعی از توابع نوسانی ساده(سینوسی، کسینوسی و یا تابع نمایی مختلط ) نوشت.این تابع به نام ریاضیدان بزرگ فرانسوی، ژوزف فوریه نامگذاری شده است. با بسط هر تابع به صورت سری فوریه، مولفه های بسامدی آن تابع به دست می آید. پیش گفتار توابع مورد استفاده در مهندسی و توابع نمایانگر سیگنالها معمولاً توابعی از زمان هستند یا به عبارت دیگر توابعی که در میدان زمان تعریف شده اند. برای حل بسیاری از مسائل بهتر است که تابع در دامنه فرکانس تعریف شده باشد زیرا این دامنه ویژگیهایی دارد که به راحتی محاسبات میانجامد. فرض کنید که تابعی به شکل زیر تعریف شده است: که در آن یک عدد صحیح مثبت، دامنه ، بسامد و فاز توابع کسینوسی می باشد. قابل مشاهده است که با در دست داشتن بسامدها ، دامنهها و فازها ...
برنامه بسط تیلور
این هم برنامه بسط تیلور که تابع sin و cos ان را حساب میکند دریافت فایل
انواع تابع
یک همسایگی باشد. تعاریف تابع هر هیچ نقطه از دامنه خود پیوسته نمیباشد. تابع تحلیلی تابع تحلیلی، تابعی است که به طور محلی به وسیله یک سری توانی همگرا مشخص می شود. می توان به توایع تحلیلی مانند یک پل بین چند جمله ایها و توابع در حالت کلی فکر کرد. اینجا توابع تحلیلی حقیقی و توابع تحلیلی مختلط وجود دارند، که شباهتها و تفاوتهایی دارند. یک تابع تحلیلی است اگر برابر با سری تیلورش در تابع f رو مجموعهٔ باز D در خط حقیقی، تحلیلی حقیقی است اگر برای هر x0 در D بتوان نوشت: در این فرمول ضرایب a0, a1, ... اعداد حقیقی هستند و سری برای x در یک همسایگی از x0 همگرا است. به صورت دیگر، یک تابع تحلیلی یک تابع بینهایت بار مشتق پذیراست به این صورت که سری تیلور در هر نقطه x0 در دامنه اش برای x به اندازه کافی نزدیک به x0 همگراست و مقدارش برابر با f(x) است. تعریف یک تابع تحلیلی مختلط با جایگزین کردن «مختلط» به جای «حقیقی» و «صفحهٔ مختلط» به جای «خط حقیقی» در مطالب بالا بدست می آید. مثال ها هر چند جملهای (حقیقی یا مختلط) یک تایع تحلیلی است. به این دلیل که اگر یک چند جمله ای از درجه n باشد، هر جمله ازدرجه بزرگتر از n در بسط سری تیلورش صفر است، وبنا براین، این سری به طور جزئی همگرا خواهد بود. تابع نمایی تحلیلی است. هر سری تیلور برای این تابع نه فقط برای x به اندازه کافی نزدیک به x0 (همان طور که در تعریف آمده) بلکه برای همه مقدار x (حقیقی یا مختلط) همگرا می شود. توابع مثلثاتی، لگاریتم و توابع توانی روی هر بازهٔ باز در دامنهٔشان تحلیلی اند. تابع قدر مطلق تحلیلی نیست زیرا مشتق پذیر نیست. توابع تعریف شدهٔ تکه ای(تابعهای معلوم به وسیله فرمولهای مختلف در مناطق مختلف) تحلیلی نیستند. خصوصیات توابع تحلیلی مجموع ها، ضرب ها و ترکیبات توابع تحلیلی، تحلیلی اند. · معکوس یک تابع تحلیلی که هیچ کجا صفر نیست، تحلیلی است. هر تابع تحلیلی هموار است. یک چند جمله ای نمیتواند در تعداد زیادی نقطه صفر باشد مگر اینکه چند جمله ای صفر باشد (به طور دقیق تر، تعداد صفرها حداکثر می تواند به اندازهٔ درجهٔ چندجمله ای باشد). حکمی مشابه ولی ضعیفتر برای توابع تحلیلی وجود دارد. اگر مجموعهٔ صفرهای تابع تحلیلی f یک نقطهٔ انباشتگی در دامنه اش داشته باشد، آنگاه f در تمام مؤلفهٔ همبندی که شامل نقطهٔ انباشتگیست صفر است. تابع هولومورفیک توابع هولومورفیک موضوع اصلی در مطالعهٔ آنالیز مختلط هستند. آنها توابعی هستند که بر روی یک زیر مجموعهٔ باز از صفحهٔ مختلط C تعریف شده اند با مقادیری در C که در هر نقطه مشتق مختلط دارند. iهولومورفيك بودن یک شرط قویتر از مشتقپذیری مختلط است و دلالت ...
اعداد مختلط
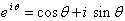
یک مطلب: ثابت میکنیم ، .(فرمول زیبا و معروف اویلر) اثبات : ابتدا ، با توجه به بسط تیلور ، توابع را به ترتیب بسط میدهیم : لازم به توضیح می باشد که توابع فوق در حول نقطه صفر بسط داده شده که به آن بسط مک لوران گفته میشود.برای اطلاعات بیشتر در مورد بسط تیلور عبارت روبرو را کلیک کنید بسط تیلور حال ، قرار میدهیم .( لازم به تذکر می باشد که i به عنوان مبنای اعداد مختلط تعریف میشود و )و در نتیجه :و در اینجا اثبات کامل است .جالب است بدانید که زیباترین فرمول ریاضی نیز ، در حالتی که در فرمول فوق، باشد بدست می آید که برابر است با .نکته دیگری هم که فکر میکنم جالب باشد اینکه ، با توجه به فرمول اویلر می توان توابع سینوسی و کسینوسی را بر حسب توابع لگاریتمی تعریف کرد ، یعنی :
