دترمینان ماتریس 3 در 3
معکوس ماتریس 3 در 3
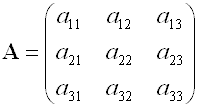
Inverse of 3x3 Matrix برای پیدا کردن معکوس ماتریس 3 در 3 ، ابتدا دترمینان آن را حساب می کنیم.اگر دترمینان مساویصفر باشد ، ماتریس معکوس وجود ندارد. محاسبه دترمینان ماتریس 3 در 3 اگر ماتریس A را بصورت زیر در نظر بگیریم : برای محاسبه دترمینان ماتریس A خواهیم داشت : det(A)=a11a22a33+a12a23a31+a13a21a32-a13a22a31-a12a21a33-a11a23a32 یا همانطور که در شکل زیر مشخص است ، ابتدا ماتریس را با تکرار دو ستون اول گسترش می دهیم و سپس درایه هایی را که با خطوط قطری به هم وصل شده اند و به آنها دسته اول می گوییم را در هم ضرب کرده و حاصلشان را با هم جمع می کنیم سپس درایه هایی را که با نقطه چین به هم وصل شده اند را در هم ضرب کرده و حاصلشان را از دسته اول کم می کنیم. ترانهاده یک ماتریس 3 در 3 بعنوان مثال برای ماتریس A ترانهاده ماتریس مانند شکل زیر می شود : محاسبه ماتریس الحاقی برای بدست آوردن ماتریس معکوس ، باید ماتریس الحاقی ماتریس A را بدست بیاوریم . برای این کار بدین گونه عمل می کنیم : ابتدا ترانهاده ماتریس A را بصورت زیر به ماتریس جدید B تبدیل می کنیم : حال درایه ها را یکی در میان در - و + ضرب میکنیم : حال معکوس دترمینان A را در B ضرب می کنیم .حاصل همان ماتریس معکوس ماتریس A است. The Inverse and Determinants of 2x2 and 3x3 Matrices The inverse of a 2x2 matrix:| a11 a12 |-1 | a22 -a12 | | a21 a22 | = 1/DET * | -a21 a11 | with DET = a11a22-a12a21 The inverse of a 3x3 matrix:| a11 a12 a13 |-1 | a33a22-a32a23 -(a33a12-a32a13) a23a12-a22a13 | | a21 a22 a23 | = 1/DET * | -(a33a21-a31a23) a33a11-a31a13 -(a23a11-a21a13) | | a31 a32 a33 | | a32a21-a31a22 -(a32a11-a31a12) a22a11-a21a12 | with DET = a11(a33a22-a32a23)-a21(a33a12-a32a13)+a31(a23a12-a22a13)
معکوس ماتریس 3 * 3 و بالاتر ( n * n )
در طی پست های قبل با نحوه به دست آوردن دترمینان یک ماتریس، ماتریس کهاد، ماتریس همسازه و ماتریس الحاقی آشنا شدیم و حالا نوبت رسیده است تا معکوس یا واران یک ماتریس را محاسبه کنیم. پیش شرط : همه می دانید که اولا ماتریس شما باید یک ماتریس مربعی باشد و دوما دترمینان آن مخالف صفر 0 باشد. اگر این دو شرط را رعایت کنید ماتریس شما واران پذیر خواهد بود.محاسبه :اگر اطلاعاتی در مورد دترمینان و ماتریس الحاقی ندارید می توانید از لینک های ابتدای پست استفاده کنید یا در اینترنت در مورد آنها جست و جو کنید چون دیگر در این پست در مورد انها صحبت نمی کنیم. فرمول زیر برای محاسبه دترمینان به کار میرود.Inv (matrix) = 1 / Det(matrix) x Adjugate-matrixInv (matrix) : ماتریس معکوسDet (matrix) : دترمینان ماتریسAdjugate-matrix : ماتریس الحاقیبه همین راحتی. پس معکوس ماتریس از ضرب عدد ( 1 تقسیم بر دترمینان ماتریس) در ماتریس الحاقی یا به عبارت دیگر از ضرب معکوس دترمینان ماتریس در ماتریس الحاقی به دست می آید. و واضح است که چون دترمینان در مخرج نشسته است، هیچگاه نمیتواند مقدار صفر داشته باشد. توضیح بیشتر همراه با مثال در مورد ماتریس 3 در 3
روشهای محاسبه دترمینان
دانش آموزان ریاضی و علاقه مندان ریاضیات تعریف اولیه دترمینان یک ماتریس مربعی از مرتبه n رو می دونن: یا که دترمینان ماتریس مربعی مرتبه n رو به دترمینان n تا ماتریس از مرتبه n - 1 تبدیل می کنه و البته برای مرتبه 2 داریم: حالا فرض کنید تابعی نوشتیم که دترمینان یک ماتریس مربعی مرتبه n رو به روش خودفراخوانی (بازگشتی) محاسبه می کنه. فکر می کنید اگه n=20 باشه ، این تابع چند بار باید خودش را فرابخونه تا بتونه دترمینان رو حساب کنه؟ مرحله توقف تابع بازگشتی رو هم n = 2 در نظر بگیرید یعنی برای n = 2 تابع مستقیما دترمینان رو محاسبه می کنه. فکر می کنید این عدد چقدر بزرگ باشه؟ حساب می کنیم: فرض کنیم ( T( n تعداد فراخوانیها برای حساب کردن دترمینان ماتریس مرتبه n باشه. واضحه که T ( 2 ) = 1 ، و همینطور: T( 3 ) = 3 T( 2 ) + 1 = 4 T( 4 ) = 4 T( 3 ) + 1 = 17 برای حساب کردن دترمینان ماتریس 3 در 3 یه بار تابع رو با n = 3 فراخوانی می کنیم . اون هم خودش سه بار تابع رو برای n = 2 فراخوانی می کنه. پس رو هم 4 بار تابع فراخوانی می شه و ... با یه حساب سر انگشتی می تونید به این نتیجه برسید که اگه n به اندازه کافی بزرگ باشه (مثلا n > 10) می شه گفت: T( n ) = n! ( e - 2 ) (e عدد نپر و !n برای فاکتوریل n) یعنی مثلا برای n = 20 تابع باید بیشتر از 1.7 میلیارد میلیارد بار (یه 17 با 17 تا صفر جلوش!!) خودش رو فراخوانی کنه تا بتونه دترمینان رو حساب کنه!!!!!! تازه اینها فقط تعداد فراخوانیها رو نشون میده. اینکه هر بار محاسبات تابع چقدر طول می کشه و چقدر حافظه نیاز هست بماند ، که اگه بخوایم اونها رو هم حساب کنیم عددمون سر به فلک می کشه!!! خوب حالا فکر می کنید کامپیوتر چطور دستگاههای بزرگ معادلات رو حل می کنه؟ محض اطلاع اون عزیزانی که اطلاع ندارن بگم توی مباحثی مثل تحقیق در عملیات و برنامه ریزی خطی ممکنه یه دستگاه معادلات 100 مجهوله داشته باشیم که اگه قرار باشه از روش بالا برای پیدا کردن جواب استفاده کنیم چند هزار سال با قویترین کامپیوتر ها طول می کشه! یکی از روشها استفاده از الگوریتم گاوس - جردن برای حل دستگاه معادلاته که در واقع اصلیترین روش به حساب می یاد و فوق العاده با صرفه تر از روش قبلیه. اکثر شما با این روش آشنا هستین و فکر نکنم نیازی به توضیح اون باشه. فقط مختصرا بگم که روش کلی اون ساده کردن معادلات دستگاه با جمع کردن ضرایب مناسبی از اونها با همه ، تا ماتریس ضرایب به یه ماتریس همانی یا بالا مثلثی یا پایین مثلثی تبدیل بشه. اما آیا روش دیگه ای وجود داره؟ اگه بخش ضمیمه کتاب «حساب دیفرانسیل و انتگرال و هندسه تحلیلی» نوشته «جرج بی. توماس و ...» رو که تو هر دانشگاه و کتابخونه ای پیدا می شه بخونید ، یه روش خیلی جالب برای محاسبه ...
بدست آوردن معکوس ماتریس
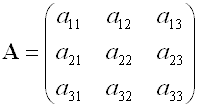
Inverse of 3x3 Matrix برای پیدا کردن معکوس ماتریس 3 در 3 ، ابتدا دترمینان آن را حساب می کنیم.اگر دترمینان مساویصفر باشد ، ماتریس معکوس وجود ندارد. محاسبه دترمینان ماتریس 3 در 3 اگر ماتریس A را بصورت زیر در نظر بگیریم : برای محاسبه دترمینان ماتریس A خواهیم داشت : det(A)=a11a22a33+a12a23a31+a13a21a32-a13a22a31-a12a21a33-a11a23a32 یا همانطور که در شکل زیر مشخص است ، ابتدا ماتریس را با تکرار دو ستون اول گسترش می دهیم و سپس درایه هایی را که با خطوط قطری به هم وصل شده اند و به آنها دسته اول می گوییم را در هم ضرب کرده و حاصلشان را با هم جمع می کنیم سپس درایه هایی را که با نقطه چین به هم وصل شده اند را در هم ضرب کرده و حاصلشان را از دسته اول کم می کنیم. ترانهاده یک ماتریس 3 در 3ش بعنوان مثال برای ماتریس A ترانهاده ماتریس مانند شکل زیر می شود : محاسبه ماتریس الحاقی برای بدست آوردن ماتریس معکوس ، باید ماتریس الحاقی ماتریس A را بدست بیاوریم . برای این کار بدین گونه عمل می کنیم : ابتدا ترانهاده ماتریس A را بصورت زیر به ماتریس جدید B تبدیل می کنیم : حال درایه ها را یکی در میان در - و + ضرب میکنیم : حال معکوس دترمینان A را در B ضرب می کنیم .حاصل همان ماتریس معکوس ماتریس A است. The Inverse and Determinants of 2x2 and 3x3 Matrices The inverse of a 2x2 matrix:| a11 a12 |-1 | a22 -a12 | | a21 a22 | = 1/DET * | -a21 a11 | with DET = a11a22-a12a21 The inverse of a 3x3 matrix:| a11 a12 a13 |-1 | a33a22-a32a23 -(a33a12-a32a13) a23a12-a22a13 | | a21 a22 a23 | = 1/DET * | -(a33a21-a31a23) a33a11-a31a13 -(a23a11-a21a13) | | a31 a32 a33 | | a32a21-a31a22 -(a32a11-a31a12) a22a11-a21a12 | with DET = a11(a33a22-a32a23)-a21(a33a12-a32a13)+a31(a23a12-a22a13)نویسنده:جوینده آزاد
بدست آوردن وارون یا معکوس یک ماتریس

مطلبی مهم را در این پست میگذارم :بدست آوردن وارون یا معکوس یک ماتریس دو در دو :یک تقسیم بر دترمینان ماتریس ضرب در (( قطر اصلی جابجا قطر فرعی برعکس ))اما مسئله مهم این است که اینجا میخواهیم معکوس ماتریس 3*3 رو بگیم : ابتدا باید یاد بگیریم که دترمینان این ماتریس چجوری بدست میاد از اینجا ( صفحه اختصاصی دترمینان خوب یاد بگیرید) حالا از فورمول زیر معکوس ماتریس رو محاسبه کنید. (اگر تصویر نمایش داده نمیشود لطفا اعلام کنید)نحوه ی حفظ کردن فورمول هم آسان است. فقط کمی دقت لازمه که چی باید از چی کم بشه یه جورایی مثل همون ماتریس دو در دو است.موفق باشید. مشکلی بود با من در ارتباط باشیدجیمیل : [email protected]هات میل:[email protected]فیسبوک :facebook.com/mohammadalighaderi20آموزش رفتن به فیس بوک بدون هیچ برنامه یا ف.ش از اینجا
راهنمایی درمورد برنامه محاسبه دترمینان ماتریس (به درخواست محمد رضا)
یا که دترمینان ماتریس مربعی مرتبه n رو به دترمینان n تا ماتریس از مرتبه n-1 تبدیل می کنه و البته برای مرتبه 2 داریم: حالا فرض کنید تابعی نوشتیم که دترمینان یک ماتریس مربعی مرتبه n رو به روش خودفراخوانی (بازگشتی) محاسبه می کنه. فکر می کنید اگه n=20 باشه ، این تابع چند بار باید خودش را فرابخونه تا بتونه دترمینان رو حساب کنه؟ مرحله توقف تابع بازگشتی رو هم n=2 در نظر بگیرید یعنی برای n=2 تابع مستقیما دترمینان رو محاسبه می کنه. فکر می کنید این عدد چقدر بزرگ باشه؟ بیاین با هم حساب کنیم: فرض کنیم T(n) تعداد فراخوانیها برای حساب کردن دترمینان ماتریس مرتبه n باشه. واضحه کهT(2)=1 و همینطور: T(3)=3T(2)+1=4 T(4)=4T(3)+1=17 برای حساب کردن دترمینان ماتریس 3 در 3 یه بار تابع رو با n=3 فراخوانی می کنیم . اون هم خودش سه بار تابع رو برای n=2 فراخوانی می کنه. پس رو هم 4 بار تابع فراخوانی می شه و ... با یه حساب سر انگشتی می تونید به این نتیجه برسید که اگه n به اندازه کافی بزرگ باشه (مثلا n>10) میشه گفت: T(n)=n!(e-2) (e عدد نپر و !n برای فاکتوریل n)یعنی مثلا برای n=20 تابع باید بیشتر از 1.7 میلیارد میلیارد بار(یه 17 با 17 تا صفر جلوش) خودش رو فراخوانی کنه تا بتونه دترمینان رو حساب کنه!!!!!! اصطلاحا گفته می شه که این روش از مرتبه O(n!) هست.تازه اینها فقط تعداد فراخوانیها رو نشون میده.اینکه هر بار محاسبات توی تابع چقدر طول می کشه و چقدر حافظه نیاز هست بماند ، که اگه بخوایم اونارم حساب کنیم عددمون سر به فلک می کشه!!! خوب حالا فکر می کنید کامپیوترا چطور دستگاههای بزرگ معادلات رو حل می کنن؟ محض اطلاع اون عزیزانی که اطلاع ندارن بگم توی مباحثی مثل تحقیق در عملیات و برنامه ریزی خطی ممکنه یه دستگاه معادلات 100 مجهوله داشته باشیم که اگه قرار باشه از روش بالا برای پیدا کردن جواب استفاده کنیم چند هزار سال با قویترین کامپیوترا طول می کشه! یکی از روشا استفاده از الگوریتم گاوس-جردن برای حل دستگاه معادلاته که در واقع اصلیترین روش به حساب می یاد و فوق العاده با صرفه تر از روش قبلیه. اکثر شما با این روش آشنا هستین و فکر نکنم نیازی به توضیح اون باشه. فقط مختصرا بگم که روش کلی اون ساده کردن معادلات دستگاه با جمع کردن ضرایب مناسبی از اونها با همه ، تا ماتریس ضرایب به یه ماتریس همانی یا بالا مثلثی یا پایین مثلثی تبدیل بشه. اما آیا روش دیگه ای وجود داره؟ اگه بخش ضمیمه کتاب «حساب دیفرانسیل و انتگرال و هندسه تحلیلی» نوشته «جرج بی. توماس و ...» رو که تو هر دانشگاه و کتابخونه ای پیدا می شه بخونید ، یه روش خیلی جالب برای محاسبه دترمینان ارائه شده که دترمینان ماتریس مرتبه n رو فقط به یه دترمینان از مرتبه ...
ماتریس
ماتریس ماتریس عبارت است از آرایشی (آرایهای) مستطیل شکل از اعداد مختلط به طوری که عناصر این آرایه را درایه مینامیم و عنصر واقع در سطر ام و ستون ام را با نماد نشان میدهیم. ماتریسی که دارای سطر و ستون باشد را ماتریس از مرتبه در مینامیم.( ) نکته هرگاه آنگاه ماتریس را مربع از مرتبه مینامیم. یک ماتریس را بصورت نمایش میدهیم. تاریخچه مطالعه روی انواع خاصی از ماتریسها مانند مربعهای جادویی و مربعهای لاتین ، به تاریخ قبل از میلاد نسبت داده شده است. معرفی و تکامل نمایش ماتریسها به عنوان شاخهای از جبر خطی در نتیجه مطلعه روی ضرایب سیستم معادلات خطی و الگوها و روشهای حل آنها بوجود آمد. لایب نیتس به عنوان یکی از پایه گذاران علم حسابان در سال 1693، دترمینان ماتریسها را معرفی کرد. در ادامه کرامر روش خود را برای حل دستگاه معادلات خطی بر اساس دترمینان ماتریس ضرایب دستگاه معرفی کرد. این روش که به روش کرامر مرسوم است، بر اساس استفاده صریح از دترمینان ماتریس ضرایب معرفی گردیده است. در مقابل اولین استفاده ضمنی از ماتریسها توسط لاگرانژ برای تعیین ماکزیمم و مینیمم توابع چند مقداری مورد استفاده قرار گرفت. در ادامه گاوس روش حذفی خود را برای حل مسائل کمترین مربعات که کاربردهای بسیار وسیعی در علوم سماوی و ژئودوزی دارد را معرفی کرد. روابط بین ماتریسها تساوی دو ماتریس دو ماتریس و مساوی اند اگر و فقط اگر (هم مرتبه باشند) و جمع دو ماتریس اگر و آنگاه قرینه ماتریس اگر آنگاه قرینه را بصورت زیر تعریف میکنیم: ضرب اسکالر در ماتریس اگر و یک اسکالر باشد آنگاهدر ضرب اسکالر یک عدد در یک ماتریس ضرب میشود. در این نوع ضرب تمامی عناصر ماتریس در آن عدد ضرب میشوند به عنوان مثال: و نمایش ریاضی آن به صورت زیر می باشد: cA)ij = c(A)ij) ضرب ماتریسها اگر و آنگاه ضرب دو ماتریس را با علامت نمایش داده و بصورت زیر تعریف خواهیم کرد: در این نوع هر دو ضرب شونده و ضرب کننده از نوع ماتریس میباشند. بطور مشابه ضرب دو ماتریس نیز باید یک جنبه خوش تعریفی داشته باشد. ضرب دو ماتریس داده شده A و B زمانی خوش تعریف است که تعداد ستونهای ماتریس ضرب کننده با تعداد سطرهای ماتریس ضرب شونده برابر باشند. بر این ضرب دو ماتریس که شرایط قابل ضرب بودن را داشته باشند به صورت زیر بیان میشود: برای بدست آوردن عنصر روی سطر iام و ستون y ام ماتریس خاصل ضرب عناصر روی سطر iام ماتریس ضرب کننده و عناصر روی ستون j ام ماتریس ضرب شونده را در نظر گرفته و آنها در هم ضرب و جمع می کنیم. به صورت ریاضی حاصلضرب دو ماتریس بصورت زیر نمایش داده می شود: A × B)ij = (A)i1(B)1j + (A)i2(B)2j + ... + ...
محاسبه دترمینان یک ماتریس
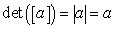
دترمینان ماتریس مربعی - که به صورت | A | یا ( det( A نمایش داده میشود - یکی از مفاهیم مشهور جبر خطی است که کاربردهای بسیاری در علوم مختلف دارد. امکان محاسبه سریع دترمینان یک ماتریس با ابعاد بزرگ، بحث مهمی است، که در ادامه سه روش محاسباتی رایج و پیچیدگی زمانی آنها مرور خواهند شد. طبق تعریف دترمینان، اگر اندازه ابعاد ماتریس مربعی یک باشد (n = 1)، دترمینان همان مقدار تکعضو آن است. یعنی: اما اگر مرتبه ماتریس بزرگتر از یک باشد (n > 1)، دترمینان را به یکی از روشهای زیر میتوان محاسبه کرد. بسط لاپلاس دترمینان بسط لاپلاس (یا بسط همسازهای) برای محاسبه دترمینان ماتریس مرتبه n، به فرم زیر است: یا که در حالت اول، بسط بر اساس سطر دلخواه i، و در حالت دوم بر اساس ستون دلخواه j صورت گرفته است. منظور از Aij (ماتریس کهاد)، ماتریسی است که از حذف سطر iام و ستون jام ماتریس اصلی به دست آمده است. به عنوان مثال، اگر ماتریس مربعی A به صورت زیر تعریف شده باشد: دترمینان آن، با بسط روی سطر اول، به این ترتیب محاسبه میشود: و با بسط روی ستون دوم: توجه داشته باشید که منظور از | | علامت قدرمطلق نیست. انتخاب سطر یا ستون مناسب برای محاسبه دترمینان با استفاده از این روش، وابسته به مقادیر درایههای آن است. به عنوان مثال، اگر تعداد درایههای صفر یک سطر یا یک ستون زیاد باشد، بهتر است از آن سطر یا ستون برای بسط استفاده کنیم. مثلا در ماتریس زیر، بهتر است از ستون اول برای بسط استفاده کنیم: پیچیدگی زمانی بسط لاپلاس همانطور که از تعریف مشخص است، در روش بسط لاپلاس، محاسبه دترمینان یک ماتریس مرتبه n، به محاسبه دترمینان n ماتریس کهاد از مرتبه n - 1 شکسته میشود. اگر عمل اصلی محاسبات را اعمال ضرب و جمع در نظر گرفته، و ( T1( n تعداد این اعمال را برای محاسبه دترمینان ماتریس مرتبه n به روش بسط لاپلاس نشان دهد، میتوان نوشت: T1( n ) = n T1( n - 1 ) + n + n + n - 1 = n T1( n - 1 ) + 3n - 1 , T1( 1 ) = 0 ( n T1( n - 1: تعداد اعمال لازم برای محاسبه زیر مسائل n: تعداد ضربهای بین aij و توانهای زوج یا فرد منفی یک n: تعداد ضربهای بین aij و ( det( Aij n - 1: تعداد جمعهای لازم برای محاسبه نهایی حل این رابطه بازگشتی نشان میدهد که ( T1( n از مرتبه ( !O( n است، که برای nهای بزرگ کارایی ندارد. روش گاوس برای محاسبه دترمینان یک ماتریس مربعی، خواصی وجود دارد که به اعمال مقدماتی سطری و ستونی مشهور بوده، و عموما از روش بسط لاپلاس ثابت میشوند. تعدادی از این خواص به شرح زیر هستند: 1- جابجا کردن دو سطر (یا دو ستون) ماتریس، مقدار دترمینان را قرینه میکند. در مثال زیر، جای سطر اول و دوم عوض شده است: 2- ...
برنامه محاسبه معکوس ماتریس n * n ( زبان C# )
در پست های قبل نحوه به دست آوردن معکوس یا واران یک ماتریس 3 در 3 یا بیشتر و همچنین شروط آن را یادآوری کردیم. در این پست هم برای کسانی که مانند من علاقه دارند برنامه محاسبه را خودشان به صورت دلخواه بنویسند، نکاتی را توضیح خواهیم داد. هدف اصلی من از این چند پست، افزایش مهارت در برنامه نویسی با بهانه تعیین معکوس یا واران یک ماتریس بود که سوژه خوبی برای برنامه نویسی در سطوح مقدماتی است؛ در این میان یک یادآوری هم از دروس دوران دبیرستان شد. در انتهای پست نیز میتوانید نسخه ای از برنامه ای که من برای این چند پست نوشته ام را داشته باشید. که به احتمال زیاد بدون مشکل نخواهد بود. اولین کار برای محاسبه معکوس ماتریس به دست آوردن ماتریس الحاقی است. ماتریس الحاقی ماتریسی هم مرتبه ماتریس ورودی است که درایه های آن از انجام 3 عملیات زیر به دست می آید : 1 : هر درایه برابر است با کهاد ماتریس نسبت به سطر و ستون آن درایه.2 : درایه های ماتریس با شرط اینکه، "اگر سطر + ستون درایه یا i+ j فرد بود" تغییر علامت می یابند. 3 : درایه های نسبت به قطر اصلی جابه جا می شوند. مانند اینکه قطر اصلی را محور تقارن ماتریس در نظر بگیریم. برای دو تغییر اول فرمول زیر استفاده می شود و ماتریسی که از این اعمال این دو تغییر به دست می یابد را ماتریس همسازه گفته می شود. A i, j = (-1) ᴵ + ᴶ x | M i ,j |من تابع محاسبه ماتریس همسازه را اینگونه نوشته ام : private double[,] Hamsaze(double[,] matrix) { int Size = (int)Math.Sqrt(matrix.Length); double[,] result = new double[Size, Size]; for (int i = 0; i < Size; i++) { for (int j = 0; j < Size; j++) { result[i, j] = Math.Pow(-1, (i+1 + j+1)) * Determinant(Kehad(matrix, i, j)); } } return result; }در این تابع دو تابع دیگر به نام Determinant و Kehad را مشاهده می کنید. که از نامشان پیداست خروجی انها چیست. تابع دترمیان :private double Determinant(double[,] matrix) { double determinant = 0; int Size = (int)Math.Sqrt(matrix.Length); if (Size == 1) { return matrix[0, 0]; } else if (Size == 2) { return (matrix[0, 0] * matrix[1, 1] - matrix[0, 1] * matrix[1, 0]); } else { for (int i = 0; i < Size; i++) determinant += (int)Math.Pow(-1, (i + 1) + 1) * matrix[0, i] * Determinant(Kehad(matrix, 0, i)); } return determinant; }تابع کهاد : private double[,] Kehad(double[,] matrix, int ROW, int COL) { int Size = (int) Math.Sqrt(matrix.Length); double[,] result = new double[Size - 1, Size - 1]; int x = -1, y = 0; for (int i = 0; i < Size; i++) { if (i == ROW) continue; x++; y = 0; for (int j = 0; j < Size; j++) { if (j == COL) continue; ...
