روش کاوالیری
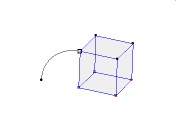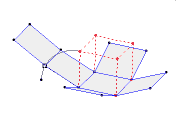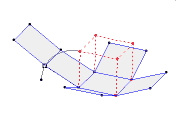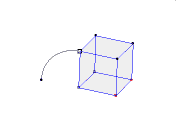
اصل کاوالیری
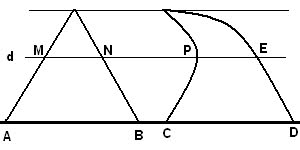
<?xml:namespace prefix = o ns = "urn:schemas-microsoft-com:office:office" /> بوتاون تورا کاوالیری (1564-1642) اهل میلان، از همان سال های نخستین به ریاضیات علاقه مند بود،و به ظاهر زیر تاثیر گالیله، روش « غیر قابل تقسیم ها» را در هندسه بوجود آورد که در اثر بزرگ او در سال 1635، با عنوان «هندسه، با طرح تازه ای بر اساس غیر قابل تقسیم های پیوسته»، به شهرت رسید. غیر قابل تقسیم ها، از نظر کاوالیری، وترهای موازی در درون شکل روی صفحه، و صفحه های موازی در درون جسم بود. او برای مقایسه ی شکل های روی صفحه و جسم های فضایی، مفهوم « مجموع همه ی غیر قابل تقسیم ها» را آورد که تماس سطح و فضای جسم را پر می کردند. برای کاوالیری، نسبت این مجموع ها، همان نسبت مساحت ها و حجم ها بود. او شکل های روی صفحه را، بین دو خط راست موازی در نظر گرفت. اصل کاوالیری درباره مساحت: اگر فرض کنیم قاعده های دو شکل بر روی یک خط قرار گرفته باشند. اگر هر خطی موازی قاعده های دو شکل در آنها قطعه هایی با طول های مساوی ایجاد کند، مساحت های آن دو شکل برابر است. با توجه به شکل دو شکل بر روی افق قرار گرفته اند. اگرهر خطی به موازات قاعده مانند d رسم کنیم و داشته باشیم: AB=CD، MN=PE ، آنگاه دو شکل هم مساحت هستند. <?xml:namespace prefix = v ns = "urn:schemas-microsoft-com:vml" /> اصل کاوالیری در باره حجم ها: دو شکل فضایی و صفحه ای که قاعده های دو شکل در آن قرار گرفته باشد را نظر بگیرید. اگر هر صفحه ای موازی با این صفحه که یکی از این دو شکل را قطع می کند، دیگری را نیز قطع می کند و سطح مقطع های حاصل دارای مساحت های برابر باشند، آنگاه این دو شکل فضایی حجم یکسان دارند. خود کاوالیری در این زمینه می نویسد: «دو جسمی که قاعده ی آنهای بر یک صفحه و ارتفاعشان برابر باشد، به شرطی هم ارزند یعنی حجم های برابر دارند که مقطع های آنهابا صفحه های موازی با قاعده باشد.» این نظام کار، به نام «نظام کاوالیری» معروف است. کاوالیری بر پایه ی این نظام، قضیه های زیادی را اثبات می کند. برای نمونه، ثابت کرد نسبت مساحت های دو مثلث متشابه برابر است با نسبت مجذور ضلع های متناظر آن ها. ابهامی که در مفهوم «مجموع غیر قابل تقسیم ها» وجود دارد، موجب اعتراض و انتقاد سخت بعضی از هم عصران کاوالیری شد. به همین خاطر کاوالیری کتاب دیگری با نام «شش طرح هندسی» را نوشت که در آن، تلاش کرد مفهوم هایی را که بکار می برد، دقیق تر کند، با وجود این، خود کاوالیری تا پایان زندگی نسبت به کافی بودن استدلالهای خود در تردید باقی بود، گرچه به درستی آن ها اعتقاد داشت. طرح کاوالیری در هندسه و آموزش او درباره ی غیر قابل تقسیم ها، تنها برای درک بهتر هندسه ی مقدماتی سودمند نبود. این آموزش، یعنی جمع کردن ...
هندسه ی کاوالیری
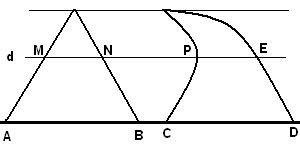
هندسه کاوالیری بوتاون تورا کاوالیری (۱۵۶۴-۱۶۴۲) اهل میلان، از همان سال های نخستین به ریاضیات علاقه مند بود،و به ظاهر زیر تاثیر گالیله، روش « غیر قابل تقسیم ها» را در هندسه بوجود آورد که در اثر بزرگ او در سال ۱۶۳۵با عنوان «هندسه، با طرح تازه ای بر اساس غیر قابل تقسیم های پیوسته»، به شهرت رسید. غیر قابل تقسیم ها، از نظر کاوالیری، وترهای موازی در درون شکل روی صفحه، و صفحه های موازی در درون جسم بود. او برای مقایسه ی شکل های روی صفحه و جسم های فضایی، مفهوم « مجموع همه ی غیر قابل تقسیم ها» را آورد که تماس سطح و فضای جسم را پر می کردند. برای کاوالیری، نسبت این مجموع ها، همان نسبت مساحت ها و حجم ها بود. او شکل های روی صفحه را، بین دو خط راست موازی در نظر گرفت. اصل کاوالیری درباره مساحت اگر فرض کنیم قاعده های دو شکل بر روی یک خط قرار گرفته باشند. اگر هر خطی موازی قاعده های دو شکل در آنها قطعه هایی با طول های مساوی ایجاد کند، مساحت های آن دو شکل برابر است. با توجه به شکل دو شکل بر روی افق قرار گرفته اند. اگرهر خطی به موازات قاعده مانند d رسم کنیم و داشته باشیم: AB=CD، MN=PE ، آنگاه دو شکل هم مساحت هستند. اصل کاوالیری در باره حجم ها دو شکل فضایی و صفحه ای که قاعده های دو شکل در آن قرار گرفته باشد را نظر بگیرید. اگر هر صفحه ای موازی با این صفحه که یکی از این دو شکل را قطع می کند، دیگری را نیز قطع می کند و سطح مقطع های حاصل دارای مساحت های برابر باشند، آنگاه این دو شکل فضایی حجم یکسان دارند. خود کاوالیری در این زمینه می نویسد: «دو جسمی که قاعده ی آنهای بر یک صفحه و ارتعاشات برابر باشد، به شرطی هم ارزند یعنی حجم های برابر دارند که مقطع های آنهابا صفحه های موازی با قاعده باشد.» این نظام کار، به نام «نظام کاوالیری» معروف است. کاوالیری بر پایه ی این نظام، قضیه های زیادی را اثبات می کند. برای نمونه، ثابت کرد نسبت مساحت های دو مثلث متشابه برابر است با نسبت مجذور ضلع های متناظر آن ها. ابهامی که در مفهوم «مجموع غیر قابل تقسیم ها» وجود دارد، موجب اعتراض و انتقاد سخت بعضی از هم عصران کاوالیری شد. به همین خاطر کاوالیری کتاب دیگری با نام «شش طرح هندسی» را نوشت که در آن، تلاش کرد مفهوم هایی را که بکار می برد، دقیق تر کند، با وجود این، خود کاوالیری تا پایان زندگی نسبت به کافی بودن استدلالهای خود در تردید باقی بود، گرچه به درستی آن ها اعتقاد داشت. طرح کاوالیری در هندسه و آموزش او درباره ی غیر قابل تقسیم ها، تنها برای درک بهتر هندسه ی مقدماتی سودمند نبود. این آموزش، یعنی جمع کردن غیر قابل تقسیم ها، پیش در آمدی برای انتگرال گیری بود. کاوالیری نماد ...
/تجربی ها و تهدید!!!/ سرشماری 6 /یک آدم فضایی/ک مثل کاوالیری/هندسه 1/ جواب مساله+تشکر/
<?xml:namespace prefix = o ns = "urn:schemas-microsoft-com:office:office" /> 1) از خودمون خیلی جای تعجب داره که خواهر آدم قالب نویس و مخ HTML باشه اما آدم یه قالب درست حسابی وبلاگش نداشته باشه!!! و بخواد تهدید های مکرر بعضیا رو در مورد قالب بشنوه!!! *راستی بنده همین جا اعلام می کنم نتایج ششمین سرشماری ملی از اعتبار کافی برخور دار نیست! چون مامانم اینا همسایه ی طبقه ی پایینمونو جا انداختن!!!! 2) از خودمون و از ریاضی و اما سوال پست پیش، با تشکر از آقای افشین منش (ریاضیات زیباست)و آقای اسماعیلی فر (لبخند ریاضی) بخاطر اثبات های قشنگی که کرده بودن... من فکر می کردم تعداد بیشتری به مساله جواب بدن! جواب مساله: الف) اثبات با استفاده از اصل لانه کبوتر اگر در میهمانی کسانی را که دست می دهندn در نظر بگیریم و به کسانی که دست نمی دهند کاری نداشته باشیم هر نفر n-1 بار یا کمتر دست می دهد (چون با توجه به صورت سوال کسی با خودش دست نمی دهد... ) حالا اگر n نفر را کبوتر و تعداد دست دادن ها که n-1 حالت دارد: n-1), (n-2), (n-3),… , 1})} ، را لانه در نظر بگیریم طبق اصل لانه کبوتری حداقل دو نفر وجود دارند که تعداد دست دادن هایشان با هم برابر است. ب) اثبات با کمک گراف جواب دوستانمون اونقدر کامل بود که دیگه من هیچی نمی گم و جوابشونو براتون می نویسم. آقای افشین منش: اگر درجه تمام روس زوج باشد که هیچ. (چون حتما دو راس با درجه مساوی خواهیم داشت- با توجه به نوع مساله). اما اگر یک راس درجه فرد داشته باشیم آنوقت الزاما باید راس دیگری از درجه فرد وجود داشته باشد (زیرا تعداد رئوس با درجه فرد در یک گراف، عددی زوج است). آقای اسماعیلی فر: اگر هر نفر رو یک راس بگیریم و هر دست دادن رو یک یال بین اونها اون وقت مساله گرافیکال میشه. حالا چون تو این گراف طوقه نداریم(کسی با خودش دست نمیده) و این گراف چندگانه است(هیچ دو نفری دوبار یا بیشتر با هم دست نمی دهند) لذا گراف حاصل گراف ساده ست. تعداد دست دادن ها براي هر نفر هم معادل درجه گراف مفروضه. قضیه: هر گراف ساده n راسي G، با حداقل دو راس داراي دو راس با درجه برابر است. اثبات: مي دانيم درجه هر راس گراف G متعلق به مجموعه 0و1و ... n-1 است. اگر دو راس از درجه برابر باشند حكم برقرار است. در غير اينصورت (فرض خلف) همه اعداد فوق درجه راسي از گراف G خواهند بود (واضحه كه با اين فرض درجه هيچ دوراسي برابر نيست). مخصوصا اينكه دو راس وجود دارند كه يكي از درجه صفر و يكي از درجه n-1 است كه اين يه تناقضه(چون اگه يك راس درجه اش n-1 باشه اونوقت به همه رئوس ديگر يك يال داره و لذا درجه بقيه رئوس حداقل يك است و صفر بودن درجه يكي از رئوس با اين مطلبي كه بيان كرديم در تناقضه). پس فرض خلف باطل است و لذا ...
زندگینامه دانشمندان
خلاصه ای از تاریخچه ریاضی و ریاضیدانان(ریاضیات در قرن ۱۷ میلادی)این قرن یکی از مهمترین قرنها در تاریخ ریاضیات است زیرا اساساْ دامنه تحقیقات گسترده در ریاضی، در همین قرن بر بشر گشوده شد، شاید به دلیل آزادیهای فکری بیشتر، پیشرفتهای سیاسی، اقتصادی و اجتماعی و در نتیجه رفاه بیشتر زندگی-به ویژه در مقابل سرما و تاریکی شمال اروپا.پیشرفت علم ریاضی در این قرن آنقدر وسیع و گوناگون است که حتی نوشتن خلاصه ای از آن نیز مثنوی هفتاد من کاغذ خواهد شد. به ناچار باید به گزینش بعضی از کارهای اصیلتر و مهم تر در تاریخ ریاضی این قرن تن داد. از مهمترین اکتشافات - و شاید هم اختراعات - ریاضی در این قرن می توان به مطالب زیر اشاره کرد:الف) کشف لگاریتمب) تدوین علامات و نمادگذاریهای کنونی جبریج) گشوده شدن پهنه جدیدی در هندسه محض به ویژه هندسه تصویرید) آغاز اتصال جبر و هندسه با کشف هندسه تحلیلیه) پیشرفتی شگرف در نظریه اعداد و نیز تولد نظریه احتمالو) کشف یکی از بزرگترین دستاوردهای بشر یعنی حساب دیفرانسیل و انتگرالشاید بهترین راه برای بررسی تاریخ ریاضی این قرن، شرح مختصری از زندگانی ریاضیدانان برجسته قرن هفدهم باشد.ریاضیدانان برجسته قرن هفدهم:1. نپر: چهار اختراع، بشر را در فن محاسبه چیره دست کرد: نماد گذاری هندی-عربی، چگونگی محاسبه مربوط به کسرها، لگاریتم و رایانه ها. «جان نپر» سومین اختراع را به نام خود ثبت کرد. او به طرز عجیبی، هم سیاسی و هم مذهبی بود و نبوغ او در پیشگویی وسایل جنگی چهار قرن بعد از خود اعجاب آور است. تعریف لگاریتم به وسیله نپر، بیشتر فیزیکی است تا ریاضی. بد نیست بدانیم که پایه لگاریتم نپر بر خلاف تصور عموم، عدد e نیست بلکه معکوس e است که البته خود او چیزی در این زمینه نمی دانست. تذکر این نکته لازم است که در تکمیل مفهوم لگاریتم و جداول مربوط به آن، «هنری بریگز» که یکی از دوستان نپر بود، سهم بسزایی دارد و لگاریتم معمولی در پایه ۱۰ را معمولاْ «لگاریتم بریگزی» می نامند. لگاریتم به معنای «عدد نسبت» است که البته این مفهوم، همان طور که ذکر شد بر اساس تابع توانی -که هم اکنون تدریس می شود- به وجود نیامد و یکی از امور خلاف قاعده در تاریخ ریاضیات، کشف لگاریتم، پیش از به کار بردن نماهاست. البته سه اختراع مهم دیگر نیز در تاریخ ریاضی، به نام جان نپر به ثبت رسیده است. (مراجعه کنید به صفحه ۴ جلد دوم کتاب تاریخ ریاضیات هاوارد د. ایوز.)2. پاسکال: این نابغه فرانسوی، یکی از بنیانگذاران هندسه محض و پیشرفته و نیز نظریه احتمال است. خواص اصلی اشکال معروف هندسی را در کودکی، بدون معلم و فقط با تلاشهای خودش به دست آورد. در شانزده سالگی ...
لگاریتم (2)

پیشینه پیشینیان ویراسنا، ریاضیدان هندی از کسانی بود که با مفهومی به نام ardhaccheda کار کرد. ardhaccheda یعنی تعداد دفعاتی که میتوان ۲n را نصف کرد. برای نمونه برای توانهای دقیق ۲ این کار برابر با لگاریتم گرفتن در مبنای ۲ بود؛ وی همچنین لگاریتم در پایهٔ دیگر اعداد صحیح مانند لگاریتم در پایهٔ ۳ (trakacheda) و در پایهٔ ۴ (caturthacheda) را نیز معرفی کرد.]مایکل استیفل در سال ۱۵۴۴ میلادی در نورنبرگ Arithmetica integra را منتشر کرد، در این نوشته جدولی از اعداد صحیح و توانهای ۲ داده شده بود، این جدول به عنوان نسخهٔ اولیهٔ جدول لگاریتم شمرده میشود. از نپر تا اویلر جان نپر (۱۶۱۷-۱۵۵۰) بدست آورندهٔ روش لگاریتمگیری روش لگاریتمگیری در سال ۱۶۱۴ از سوی جان نپر در کتابی با عنوان Mirifici Logarithmorum Canonis Descriptio (توصیفی بر قانون شگفتانگیز لگاریتم) ارائه شد.همچنین ژو بورجی (به فرانسوی: Joost Bürgi) نیز جداگانه روش لگاریتمگیری را پیدا کرده بود اما آن را شش سال پس از نپر منتشر کرد. نپر، با استفاده از روش تقسیمهای متوالی توانسته بود عبارت را به ازای Lهای میان ۱ تا ۱۰۰ محاسبه کند. جواب این عبارت برای ۱۰۰ = L تقریبا برابر است با ۰٫۹۹۹۹۹ = ۱ - ۵-۱۰ و ۲۰ ۰٫۹۹۵ ≈ ۰٫۹۹. این محاسبات که ۲۰ سال طول کشید، باعث شد تا او بتواند به ازای هر عدد N در بازهٔ ۵ تا ۱۰ میلیون، بتواند عدد L را پیدا کند که در رابطهٔ زیر صدق کند: نپر ابتدا نام «عدد ساختگی» را بر L نهاد ولی پس از مدتی واژهٔ «لگاریتم» logarithm را معرفی کرد و آن را بر عددی گذاشت که نمایندهٔ یک نسبت است: واژهٔ λόγος برابر logos به معنی «نسبت» است و واژهٔ ἀριθμός برابر arithmos به معنی «عدد» است. بوسیلهٔ عبارت زیر میتوان مفهوم پیشین لگاریتم را با مفهوم امروزی لگاریتم طبیعی مرتبط کرد: با تقریب خوبی داریم: این دستآورد خیلی زود مورد تحسین گستردهٔ دیگران قرار گرفت، به همین دلیل با تلاش دانشمندانی چون بوناونتورا کاوالیری (Bonaventura Cavalieri) از ایتالیا، ادموند ونگت (Edmund Wingate) از فرانسه، زو فنگزوئو (Xue Fengzuo) از چین و... مفهوم لگاریتم همه جا فراگیر شد. هذلولی y = ۱/x (منحنی قرمز) و سطح زیر آن از x = ۱ تا ۶ (قسمت نارنجی رنگ). در سال ۱۶۴۷ گرگوآر دو سن-ونسان توانست مفهوم لگاریتم را با یک چهارم هذلولی مرتبط کند، با فرض آنکه سظح زیر منحنی هذلولی به ازای ۱ = x تا t در رابطهٔ زیر صدق میکند: لگاریتم طبیعی اولین بار از سوی نیکولاس مرکاتور در مقالهٔ Logarithmotechnia که در سال ۱۶۶۸ منتشر کرد، توضیح داده شد. البته پیش از او جان اسپیدل که یک معلم ریاضی بود در سال ۱۶۱۹ جدولی از لگاریتم طبیعی را گردآوری کرده بود. در حدود سال ۱۷۳۰ لئونارد اویلر تابع نمایی ...
قضیه ی دزارگ
هِندِسه مطالعه انواع روابط طولی و اشکال و خصوصیات آنها است. این دانش همراه با حساب یکی از دو شاخه قدیمی ریاضیات است. واژه هندسه عربی شده واژه «اندازه» در فارسی است. در زبان انگلیسی به آن geometry و در زبان فرانسه به آن géométrie میگویند که هردو از γεωμετρία (گئومتریا) در زبان یونانی آمده که به معنای اندازهگیری زمین است.تاریخچه هندسهاحتمالاً بابلیان و مصریان کهن نخستین کسانی بودند که اصول هندسه را کشف کردند. در مصر هر سال رودخانه نیل طغیان میکرد و نواحی اطراف رودخانه را سیل فرا میگرفت. این رویداد تمام علایم مرزی میان املاک را از بین میبرد و لازم میشد دوباره هر کس زمین خود را اندازهگیری و مرزبندی کند. مصریان روش علامتگذاری زمینها با تیرک و طناب را ابداع کردند. آنها تیرکی را در نقطهای مناسب در زمین فرو میکردند و تیرک دیگری در جایی دیگر نصب میشد و دو تیرک با طنابی که مرز را مشخص میساخت به یکدیگر متصل میشدند. با دو تیرک دبگر زمین محصور شده و محلی برای کشت یا ساختمان سازی مشخص میشد.در آغاز هندسه برپایه دانستههای تجربی پراکندهای در مورد طول و زاویه و مساحت و حجم قرار داشت که برای مساحی و ساختمان و نجوم و برخی صنایع دستی لازم میشد. بعضی از این دانستهها بسیار پیشرفته بودند مثلاً هم مصریان و هم بابلیان قضیه فیثاغورث را ۱۵۰۰ سال قبل از فیثاغورث میشناختند. یونانیان دانستههای هندسی را مدون کردند و بر پایهای استدلالی قراردادند. برای آنان هندسه مهمترین دانشها بود و موضوع آن را مفاهیم مجردی میدانستند که اشکال مادی فقط تقریبی از آن مفاهیم مجرد بود. در سال ۶۰۰ قبل از میلاد مسیح، یک آموزگار اهل ایونیا (که در روزگار ما بخشی از ترکیه بهشمار میرود) به نام طالس، چند گزاره یا قضیه هندسی را به صورت استنتاجی ثابت کرد. او آغازگر هندسه ترسیمی بود. روش استنتاجی روشی است علمی (بر خلاف روش استقرایی) که در آن مسالهای به وسیلهی قضایا و حکمها ثابت می گردد. فیثاغورث که او نیز اهل ایونیا و احتمالاً از شاگردان طالس بود توانست قضیهای را که بهنام او مشهور است اثبات (ریاضی) کند. البته او واضع این قضیه نبود. اما دانشمندی به نام اقلیدس که در اسکندریه زندگی میکرد، هندسه را به صورت یک علم بیان نمود. وی حدود سال ۳۰۰ پیش از میلاد مسیح، تمام نتایج هندسی را که تا آن زمان شناخته بود، گرد آورد و آنها را به طور منظم، در یک مجموعه ۱۳ جلدی قرار داد. این کتابها که اصول هندسه نام داشتند، به مدت ۲ هزار سال در سراسر دنیا برای مطالعه هندسه به کار میرفتند. براساس این قوانین، هندسه اقلیدسی تکامل ...
تاریخچه ی ریاضیات
اولین سمینار منطقه ای ریاضی تـاریـخـچـه ی ریـاضـیـات حسین شجاعی وند تجرق مقطع و گرایش: کارشناسی _ ریاضی کاربردی www.mathhossein.blogfa.com [email protected] 0914 – 921 – 1676 تاریخچه ی ریاضیات قسمت اول: (از قبل میلاد تا قرن پنج میلادی) انسان اولیه نسبت به اعداد بیگانه بود و شمارش اشیاء اطراف خود را به حسب غریزه یعنی همانطور که مثلاً مرغ خانگی تعداد جوجههایش را میداند انجام میداد. اما بزودی مجبور شد وسیلة شمارش دقیقتری بوجود آورد. لذا، به کمک انگشتان دست دستگاه شماری پدید آورد که مبنای آن 60 بود.این دستگاه شمار که بسیار پیچیده میباشد قدیمیترین دستگاه شماری است که آثاری از آن در کهنترین مدارک موجود یعنی نوشتههای سومری مشاهده میشود. سومریها که تمدنشان مربوط به حدود هزار سال قبل از میلاد مسیح است در جنوب بینالنهرین، یعنی ناحیه بین دو رود دجله و فرات ساکن بودند. آنها در حدود 2500 سال قبل از میلاد با امپراطوری سامی، عکاد متحد شدند و امپراطوری و تمدن آشوری را پدید آوردند. در این موقع مصریها نیز در سواحل سفلای رود نیل تمدنی درخشان پدید آورده بودند. طغیان رود نیل هر سال حدود و ثغور زمینهای زراعتی این قوم را محو میکرد. احتیاج به تقسیم مجدد این اراضی موجب رهبری آنها به اولین احکام سادة هندسی گردید. همچنین مبادلات تجارتی و تعیین مقدار باج و خراج سالیانه آنها را وادار به توسعه علم حساب نمود این اطلاعات همگی از روی پاپیروسها و الواحی است که در نتیجه حفاریها بدست آمده و به خط هیروگلیفی میباشد. قدیمیترین آنها که مربوط به 1800 سال قبل از میلاد است شامل چند رساله دربارة علم حساب و مسائل حساب مقدماتی میباشد، از آن جمله رسالة پاپیروس آهس است که درسال 1868 توسط ایسنلر مصرشناس مشهور ترجمه شد. سایر تمدنهای شرقی نظیر چینی و هندی در ترویج دانش نقش مؤثری نداشتهاند و جز برخی نتایج پراکنده که در زیر فشار مفاهیم ماوراءالطبیعه خرد شده است چیزی از آنان در دست نیست. قریب هزار سال پس از نابودی فرهنگ قدیم مصر و محو تمدن آَشور، یونانیان از روی مقدمات پراکنده و بیشکل آنها علمی پدید آوردند که در واقع به عالیترین وجه مرتب و منظم گردیده و عقل و منطق را کاملاً اقناع مینمود. نخستین دانشمند معروف یونانی طالس ملطلی (639_548ق.م) است که در پیدایش علوم نقش مهمی بعهده داشته و میتوان ویرا موجد علوم فیزیک ، نجوم و هندسه «تشابه» به او کاملاً بیاساس است. در اوایل قرن ششم ق.م. فیثاغورث (572_500 قبل از میلاد) از اهالی ساموس یونان کمکم ریاضیات را بر پایه و اساسی قرار داد و به ایجاد مکتب فلسفی خویش همت گماشت. فیثاغورثیان عدد را بخاطر همآهنگی ...
مباحث مهم آزمون 21 آذر قلم چی
مباحثی که برای آزمون 21 آذر قلم چی حتما باید بخونید ... اولویت با مباحثی است که گذاشته شده است و بخش های غیر مهم حذف شده است تا بتوانید برای نیم سال اول آماده شوید و کمی از عقب ماندگی ها را جبران کنید و با این مباحث می توان تا تراز 7000 را آورد. مباحث اولیه هر کتاب پیش معمولا اول سال خوب خوانده شده است و بهتر است با این آزمون بیشتر روی دیگر بخش ها توجه کنید در ضمن با این کار در آزمون های دی ماه می توانید کل پیش 1 را جمع بندی کنید عمومی : ادبیات 2: صفحه 100 تا 122 زبان فارسی: نگارش ( آشنایی با نوشته های ادبی) عربی 2: صفحه 53 تا 108 دینی 2: صفحه 76 تا 109 ادبیات پیش : ادبیات حماسی دینی پیش : حقیقت بندگی + در مسیز اخلاص و قدرت پرواز زبان پیش : صفحه 1 تا 32 اختصاصی تجربی: زمین شناسی: زمین لرزه ریاضی عمومی : توابع + معادلات ریاضی پایه : فصل 4 هندسه ( اگر سخت است می توان احتمال را خواند و از فصل چهار فقط اصل کاوالیری را بخواندید) زیست پیش : پیدایش و گسترش زندگی + تغییر و تحول گونه ها + ژنتیک و جمعیت زیست پایه : ژنتیک و خواستگاه فیزیک پیش : دینامیک + حرکت نوسانی تا صفحه 60 فیزیک 2 : کار و انرژی شیمی پیش : تعادل شیمیایی شیمی 2: ترکیب های کووالانسی اختصاصی ریاضی: دیفرانسیل :حد و پیوستگی ریاضی پایه : توابع و انواع آن ، نامعادله و تعیین علامت هندسه تحلیلی : مقاطع مخروطی دایره گسسته : گراف یا نظریه اعداد ( هر کدام که راحت تر است) فیزیک پیش : دینامیک و حرکت نوسانی تا صفحه تا صفحه 77 شیمی پیش : تعادل شیمیایی هندسه 1 : هندسه فضایی فیزیک 2: کار و انرژی شیمی 2: ترکیب کووالانسی یک برگه جهت نوشتن برنامه ریزی آزمون در زیر گذاشته ام که دانلود کنید. جهت دانلود کلیک کنید جهت برنامه ریزی روزانه می توانید به شماره زیر پیغام دهید. 09356487825 مجتبی لشینی
آموزش کامل لگاریتم
نمودار لگاریتم در پایهٔ ۲ که محور xها (محور افقی) را در نقطهٔ ۱ قطع میکند، بالا میرود و به ترتیب از نقطههای (۲،۱) و (۴،۲) و (۸،۳) عبور میکند. به ازای اعداد نزدیک صفر، منحنی لگاریتم به محور عمودی y بسیار نزدیک میشود ولی هرگز با آن مماس نمیشود یا آن را قطع نمیکند. لُگاریتم یک عدد در یک پایه، برابر با توانی از پایهاست که آن عدد را میدهد. برای نمونه لگاریتم ۱۰۰۰ در پایه ۱۰، برابر با ۳ است. چون ۱۰ × ۱۰ × ۱۰ = ۱۰۰۰ یا به بیان کلیتر اگر x = by باشد آنگاه لگاریتم x در پایهٔ b برابر با y خواهد بود و به زبان ریاضی آن را به صورت نمایش میدهیم. مانند: لگاریتم نخستین بار از سوی جان نپر در اوایل سده ۱۷ میلادی به عنوان وسیلهای برای آسان تر کردن محاسبات، معرفی شد؛ که به سرعت از سوی دانشمندان و مهندسان پذیرفته شد و برای آسانتر کردن و سریعتر کردن محاسبه جدولهای لگاریتم اعشاری و خطکشهای لغزنده ایجاد شدند و مورد استفاده قرار گرفتند. تمامی این ابزارها بر پایهٔ این مفهوم که «لگاریتم حاصل ضرب برابر است با مجموع لگاریتمها»، ساخته شده بودند: مفهوم امروزی لگاریتم از تلاشهای لئونارد اویلر در قرن ۱۸ گرفته شده است؛ او توانست مفهوم لگاریتم را با مفهوم تابع نمایی پیوند دهد. لگاریتم در پایه ۱۰ را لگاریتم اعشاری مینامند که کاربرد بسیار زیادی در مهندسی دارد. لگاریتم در مبنایثابت e یا عدد نپر ≈ ۲٫۷۱۸ را لگاریتم طبیعی مینامند. این لگاریتم در ریاضیات محض بویژه حساب دیفرانسیل و انتگرال بسیار کاربرد دارد. لگاریتم دو دویی نیز در مبنای ۲ نوشته میشود و کاربرد زیادی درعلوم رایانه دارد. به کمک مقیاس لگاریتمی، میتوان اندازههای بسیار بزرگ را در ابعاد بسیار کوچکتری نشان داد برای نمونهدسیبل یکایی لگاریتمی است که برای نشان دادن فشار صدا و نسبت ولتاژ کاربرد دارد. در شیمی نیز پ هاش که معیاری برای نشان دان میزان اسیدی بودن مایعات است در مقیاس لگاریتمی بیان میشود. همچنین لگاریتم در نظریه پیچیدگی محاسباتی و در برخی شکلهای هندسی مانند برخالها کاربرد دارد. از دیگر کاربردهای آن میتوان به فاصله در موسیقی و رابطههای شمارش اعداد اول اشاره کرد. تابع توان وارون تابع لگاریتم است و لگاریتم مختلط، تابع وارون تابع نمایی به کار رفته در اعداد مختلط است. لگاریتم گسسته نیز در رمزنگاری کلید عمومی استفاده میشود. انگیزه اولیه و تعریف انگیزه ساخت لگاریتم، داشتن وارون تابع توان بودهاست. برای نمونه، توان سوم ۲، ۸ است چون ۸ = ۲ × ۲ × ۲ = ۲۳ پس لگاریتم ۸ در پایهٔ ۲، ۳ میشود. به توان رساندن توان ...
هندسه یک – هندسه دو – هندسه تحلیلی
هندسه یک – هندسه دو – هندسه تحلیلی این کتاب عظیم هستی برای همیشه در جلوی چشمهای ما گشوده شده است و زبانی دارد ، اما بدون دانستن آن ، فهم حتی یک واژه هستی غیرممکن می نماید. آن زبان ، ریاضی است .(گالیله) آموزش هندسه 1 1- هندسه و استدلال : - کشف اطلاعات از طریق مشاهده - کشف اطلاعات از طریق تجربه - استدلال در هندسه- مثلث های همنهشت - مثلث متساوی الساقین - از خم ساده تا چند ضلعی - متوازی الاضلاع 2- مساحت و قضیه فیثاغورس : - مساحت - قضیه فیثاغورس 3- تشابه : - نسبت و تناسب- قضیه تالس در مثلث - مثلث های متشابه- حالت های تشابه دو مثلث- پاره خط های متناسب دردو مثلث متشابه- محیط و مساحت شکل های متشابه 4- شکلهای فضایی : - خط و صفحه در فضا- مکعب مستطیل - منشور و استوانه- اصل کاوالیری ، حجم منشور و استوانه- هرم و مخروط - کره آموزش هندسه 2 1- استدلال در هندسه : - استدلال استقرایی- استدلال استنتاجی - مثال نقض- قضیه های شرطی- عکس قضیه - اثبات غیر مستقیم یا برهان خلف- مکان هندسی - ترسیم با خط کش و پرگار 2- دایره : - زاویه مرکزی ، وتر و مماس- خط های قاطع و مماس نسبت به دایره- وضع دو دایره نسبت به هم - زاویه محاطی- زاویه ظلی - کمان در خور یک زاویه - زاویه بین دو وتر - زاویه بین امتداد دو وتر- رابطه طولی در دایره - ترسیم های هندسی 3- تبدیل ها: - نگاشت- انتقال- بازتاب - دوران- تجانس - تبدیل یافته خط و معادله آن - اثبات با استفاده از ویژگی های تبدیل ها 4- هندسه در فضا : - خط و صفحه در فضا - صفحه در فضا - وضعیت دو صفحه نسبت به هم در فضا- وضعیت دو خط نسبت به هم در فضا- وضعیت خط و صفحه نسبت به هم در فضا- خط ها و صفحه های موازی- خط و صفحه موازی- چند ویژگی از خط ها و صفحه های موازی- صفحه های موازی- زاویه بین دو خط در فضا- خط ها و صفحه های عمود بر هم - خط عمود بر صفحه- کاربرد تعامد در حل مساله های توازی- صفحه عمود منصف یک پاره خط- دو صفحه عمود بر هم - فاصله نقطه از صفحه- عمود مشترک دو خط متنافر آموزش هندسه تحلیلی و جبر خطی 1- بردارها : - معرفی فضای سه بعدی- بردارها در فضای سه بعدی - تعبیر هندسی- بردارهای یکه - ضرب داخلی- ویژگی های ضرب داخلی- ضرب خارجی - ویژگی های ضرب خارجی - مساحت متوازی الاضلاع - حجم متوازی السطوح 2- معادلات خط و صفحه : - خط در فضا - فاصله یک نقطه از یک خط - وضعیت نسبی دو خط در فضا- صفحه در فضا- فاصله یک نقطه از یک صفحه - وضعیت نسبی دو صفحه در فضا - وضعیت نسبی یک خط و یک صفحه در فضا 3- مقاطع مخروطی : - دایره - بیضی- سهمی - هذلولی- انتقال محور های مختصات- دوران محور های مختصات 4- ماتریس و دترمینان : - ماتریس ها - جمع ماتریس ها و ضرب اعداد حقیقی در آن ها - ضرب ماتریس ها- ترانهاده یک ماتریس ...
